We Learn   We Create   We Share

初学者指南
笔记
竞赛
关于我们
页面搜索

目录

代价统一搜索 Uniform Cost Search

Algorithm Notes

Mark Chen | 29 Apr 2021

你使用哪种语言？我们会根据你选择的语言显示对应的代码示例

Python
Java

前置条件

代价统一搜索策略

在之前的深度优先搜索和广度优先搜索中，我们一般都只考虑目标节点与出发节点之间的图上距离1而非真实距离2 - 这在一些简单的场景下没有什么问题，但是在一些情况下图上的距离与真实距离并不一致。例如下图：

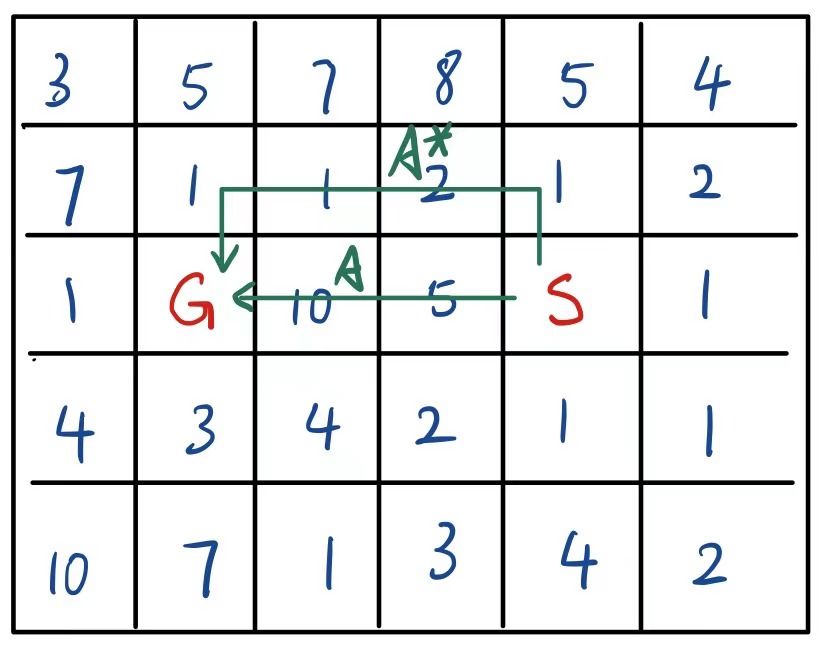
6e5f63b38286cc81fc07f61886fabb9

在下面这张图中， $G$ 与 $S$ 之间的图上距离最小路径应该是直线 $A$。但是，如果我们要看 $G$ 和 $S$ 之间的路径权重之和最小的话我们会发现最优路径并不是 $A$ 而是 $A*$，因为 $A$ 的路径权重之和为 $10 + 5 = 15$ 而 $A*$ 的路径权重之和为 $1 + 2 + 1 + 1 = 5$。

为了找到实际距离最短的路径而不是图上距离最短的路径，人们在 BFS 的基础上做出了改动，产生了更加准确的 UCS 代价统一搜索策略。在 BFS 中，Queue 的性质距离初始节点图上距离最小的节点会优先被展开，而在 UCS 中，我们用 Priority Queue 实现 Fringe，这个优先队列对待探索节点的排序是基于初始节点到待探索节点的实际距离决定的。

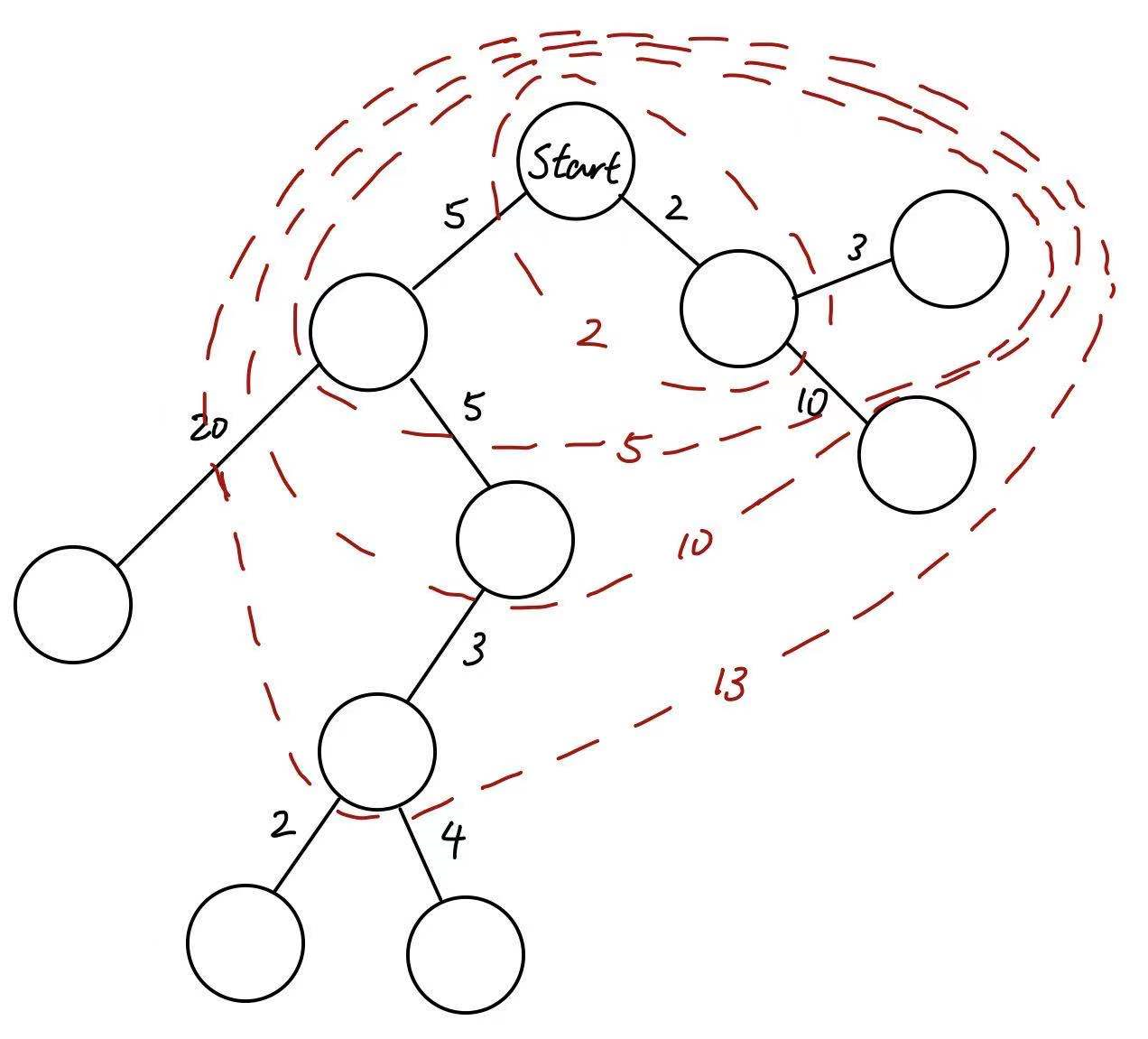
一张图的 “等 Cost 线“

在 UCS 对图像进行遍历的过程中，如果在 Fringe 中 Actual Cost 最小的节点的 Actual Cost 为 $C$，则所有已探索的节点的 Actual Cost 都一定$\leq C$。通过这个性质，我们可以轻易证明UCS找到的第一个目标节点一定是距离初始节点实际距离最小的目标节点（即最优解）。

代价统一算法的实现

    
import heapq    # The Python Module for Priority Queue

def uniformCostSearch(initialState, getSuccessor, getValidActions, getActionCost):
    """
    :param initialState: The Initial State of problem (sometimes the 'current state')
    :param getSuccessor: The State Transition Function that return the successors given the current state and action
    :param getValidActions: A function that takes current state and return a list of valid actions under current state
    :param getActionCost: A function that will return cost of action given action and current state
    """
    fringe = []    # The only difference between BFS and DFS
    exploredStates = set()
    
    # Add the Initial State into the Fringe before Searching Actually Start.
    # Instead of storing state directly in the fringe, we will use a tuple to store state, where the 
    # 0th param of tuple is cumulative cost
    # 1th param of tuple is the state
    
    heapq.heappush(fringe, (0, initialState))	# The initial cost is 0
    while len(fringe) > 0:
    	cost, currState = heapq.heappop(fringe)
        if currState in exploredStates: continue
        else: exploredState.add(currState)
            
        # Do Something Here
        
        for action in getValidActions(currState):
            # Add Successor States into the fringe
            successor = getSuccessor(currState, action)
            if successor not in exploredStates:
                deltaCost = getActionCost(currrState, action)
                heapq.heappush((cost + deltaCost, successor))
    
    
Not Implemented Yet, see Python Version

练习

暂无练习 （一般与其他算法搭配使用，很少有单独的练习出现，思考一下之前做过的一些 BFS / DFS 题目有没有可能用 UCS 取代原来的算法来优化？）

  1. 图上距离指节点之间的边的数量 ↩

  2. 真实距离指节点之间的边的权重之和 ↩

评论区