时间复杂度

Algorithm Notes

Mark Chen | 02 Mar 2021

你使用哪种语言？我们会根据你选择的语言显示对应的代码示例

Python

Java

在编程竞赛中，你提交的代码一般会有运行时间限制 - 程序只有在规定的时间内运行完毕并返回正确的结果才能得到对应的分数。如果程序不能在规定时间内运行完毕则会触发超时错误 (TLE, Time Limit Exceed)。

具体来说，USACO 对 C++ 的运行时间要求是 2 秒，Java 和 Python 则要在 4 秒内运行完毕。一般认为 USACO 的运行服务器每秒可以进行 $1\times 10^{8}$ 次基本操作¹。

因为有运行时间的限制，如果我们可以在比赛的时候先分析算法的时间复杂度再实现，就可以避免浪费很多时间在 TLE 的问题上。

⚠一般铜组的题目不会出现算法时间超时的情况。（用USACO官方的话说：在一些题目中即使所有排序算法都用最慢的$O(n^2)$实现也不会导致TLE）如果你在铜组遇到了TLE，你应该优先考虑自己是不是不小心写了无限循环。

虽然在较为初级的题目中 TLE 基本不会发生，但是我们依然把这个知识点放在相当靠前的位置，因为时间复杂度是算法非常重要的一个指标。只有在一开始就树立这个概念后面才能较为流畅的使用这个工具分析自己的代码。

渐进分析与大$O$记号

渐进分析研究函数 $f(n)$ 是如何随着 $n \rightarrow \infty$ 变化的。大 $O$ 记号是一种描述函数增长趋势的方法。

如果我们说 $f(n)\in O(n^2)$，我们的意思是一定存在一个函数 $g(n) = cn^2$，使得对于任意常数$x$ 与 $c$，只要 $n\gt x$ ， $f(n) < g(n)$ 一定成立。

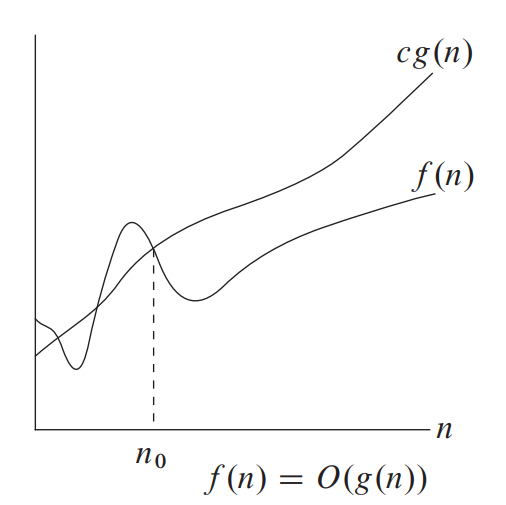
如上图所示，如果我们说函数 $f(n)$ 是 $O(g(n))$ 时，并不意味着对于所有 $n$ 都有 $cg(n) > f(n)$。这只意味着对于一个特定的常数 $n_0$，只要 $n > n_0$，我们都有 $cg(n) > f(n)$。

显然，当我们描述一个函数的打O记号时，我们只需要描述函数的最高此项即可，因为其他项对函数的值的影响相对会小很多。

\[f(n) = 2n^3 + n^2 - n + 10\\ f(n) \in O(n^3)\]

上面的结论 $f(n) \in O(n^3)$ 是正确的，因为对于超过一个常数值的任意 $n$，我们显然有 $f(n) < 3n^3$

如果你想看更多关于渐进分析的知识，例如 $\Theta(f(n))$, $\Omega(f(n))$ 等的话可以在这里看看。【链接】

复杂度计算

我们需要一种方法去描述算法的运行步骤如何随着输入数据的大小 $n$ 变化。通过大 $O$ 记号，我们可以很方便的描述一个算法处理大小为 $n$ 的数据所需要的时间时如何随着 $n$ 的变化而变化的。

    
a = 0
b = 1
c = 20
print(a + b + c)
    
    
public static void main(String[] args){
    int a = 0;
    int b = 1;
    int c = 20;
    System.out.println(a + b + c);
}

上面这个代码的时间复杂度是 $O(1)$，因为程序的计算步骤无论什么情况都是固定的。

如果有一个循环，那么时间复杂度与循环的循环次数有关 - 例如下面的这个代码的时间复杂度是 $O(n)$

    
n = int(input())
for i in range(0, n):
    # some O(1) time code in the loop
    print("Loop #"+str(i))
    
    
int n = 100;
for (int i = 0; i < n; i ++){
    System.out.println(i);
}

如果有多个循环嵌套的话，那么各个嵌套的循环的时间复杂度应该直接相乘，例如下面这个代码的时间复杂度是 $O(mn)$

    
for i in range(n):
    for k in range(m):
        # O(1) Code inside here.
        print(i, k)
    
    
for (int i = 0; i < n; i ++){
    for (int j = 0; j < m; j ++){
        // O(1) Code Inside Here.
        System.out.println(j);
    }
}

上面的代码的时间复杂度是 $O(mn)$ 因为里面的 $O(m)$ 代码被运行了 $O(n)$ 次

在一个算法中，如果有很多部分的话，整个算法的时间复杂度是所有部分中最高复杂度的部分。

    
# This Part of Code has time complexity of O(mn)
for i in range(n):
    for k in range(m):
        # O(1) Code inside here.
        print(i, k)

# This Part of Code has time complexity of O(m)
count = 0
for i in range(m):
    count += i
    
    
public static void main(String[] args){
    // This Part of Code has Time Complexity of O(mn)
    for (int i = 0; i < n; i ++){
        for (int j = 0; j < m; j ++){
            // O(1) Code Inside Here.
            System.out.println(j);
        }
    }

    // This Part of Code has Time Complexity of O(m)
    for (int k = 0; k < m; k ++){
        System.out.println(k);
    }
}

在这段代码中，第一部分的复杂度是 $O(mn)$，第二部分的复杂度是 $O(m)$，因为我们之前提到大O记号是只看最高此项的，整个代码的复杂度是 $O(mn)$。

常见的时间复杂度

如果你不认识下面的这些算法，没关系，后面我们会介绍这些算法

算法	时间复杂度
数学计算（标量积算）	$O(1)$
二分查找	$O(\log{n})$ （每次查找）
优先队列	$O(\log{n})$ （每次添加/减少）
素性检测，因式分解	$O(\sqrt{n})$
读取 $n$ 行输入	$O(n)$
遍历 $n$ 个元素的队列	$O(n)$
排序算法	$O(n\log{n})$ （一般情况下）
一些特殊的排序算法²	$O(n^2)$
遍历一个集合中所有的子集	$O(2^n)$
遍历所有的排列组合	$O(n!)$

数据规模与时间复杂度

USACO 和 CCC 的编程题的时间限制都是4秒左右。在这段时间内，服务器可以进行大约 $1\times 10^9$ 次基本操作。这意味着什么？下面这张表格列举出来了不同时间复杂度能在时间限制内运行完毕的数据规模

时间复杂度	在规定时间内可以完成计算的数据规模
$O(n!)$, $O(n^m), \text{where }m > 5$	$n\leq 10$
$O(n\cdot 2^n)$,$O(n^5)$	$n\leq 20$
$O(n^3)$	$n\leq 500$
$O(n^2)$	$n\leq 7500$
$O(n \sqrt{n})$	$n\leq 7\times 10^4$
$O(n\log{n})$	$n\leq 5\times 10^5$
$O(n)$	$n\leq 5\times 10^6$
$O(1)$, $O(\log{n})$	$n\leq 10^{18}$