Binary Index Tree (Fenwick Tree) 二叉索引树

Algorithm Notes

---

Mark Chen | 09 May 2021

报告错误

如果你发现该网页中存在错误/显示异常，可以从以下两种方式向我们报告错误，我们会尽快修复：

1. 使用 CS Club 网站错误 为主题，附上错误截图或描述及网址后发送邮件到 286988023@qq.com
2. 在我们的网站代码仓库中创建一个 issue 并在 issue 中描述问题 点击链接前往Github仓库

前置技能

• 理论基础：时间复杂度 Time Complexity
• 算法：递归 Recursion
• 数据结构：二叉树 Binary Tree
• 数据结构：前缀和 Prefix Sum

Python Version not Implemented Yet.

Traditional Approach 1

在实际生活中，我们常常需要计算一个给定array 特定范围内所有数的和。如果只有这一个需求的话，我们可以很方便的构建出一个静态的数组来达到$O(1)$的时间复杂度。在这样的一个数组中，每一个位置上的数符合：

这样，当我们需要计算数列x中m到n的数字的和时，我们只用计算 arr[n] - arr[m]就可以了。

然而，与计算的超高性能相比，这种方法要求我们操作的数列x是基本保持不变的，一旦x中的某一个值发生了变化，我们就要更新一次整个arr数组，这直接导致了修改的$O(n)$复杂度。

Traditional Approach 2

如果我们想要我们的数据结构可以接受大量的修改，我们也可以使用一个更加朴素的方法 - 我们只存储数列x，每次要计算区间和时，我们就遍历一次整个区间从而计算区间内所有元素的和。

使用这种朴素的方法，虽然计算区间和的复杂度位$O(n)$，每次我们对数组x进行修改却不需要额外的操作，只有$O(1)$的复杂度。

Why Traditional Approach Fail

我们知道，一个算法的时间复杂度是由算法中最耗时间的步骤所决定的，也就是说，如果我们在一个循环中同时需要查询数组x的区间和并且修改x，那么整个循环内的时间复杂度会由其中最耗时间的步骤决定 - $O(n)$。

二进制索引树被设计出来处理这种情况，它很好的在两种传统方法间做出取舍，使得我们可以同时以$O(\log{n})$的时间复杂度进行数组的修改和区间和查询操作。

Data Structure - BIT

虽然BIT的名字是“二叉索引树”，实际上在程序中，我们并没有使用一个“树”的结构去存储BIT对象，而是将其放在一个数组中，这种结构被称为“树状数组”，许多树结构也使用了这样的形式 - 例如二叉堆模型。

这是一个BIT数据结构的内部属性：

public class BinaryIndexTree{
    private int[] tree;
    private int[] val;
    
    // ...
    
}

BIT之所以中间有一个“index”，是因为BIT的构造和操作过程中都要使用索引的一个属性 - 索引( + 1后)二进制中最后一个1的位置。

Helper Function - Least Significant One

在 Java 中，我们可以写一个这样的函数来找到整数二进制最后一位的1在哪里：

public int findLastBinaryOne(int index){
    String binaryIndex = Integer.toBinaryString(index + 1);
    for (int i = binaryIndex.length() - 1; i > -1; i --){
        if (binaryIndex.substring(i, i + 1).equals("1")){return binaryIndex.length() - i;}
    }
    return -1;
}

通过计算索引 + 1后的二进制的最后一位1在哪里，我们可以得到BIT中这个位置的节点在树中的高度。

Construct BIT

如果findLastBinaryOne 返回为1，数组中这个位置是BIT的叶子节点，只存储输入数列x在这个位置的值（例如在下图中的 index = 0, 2, 4, 6, …）的位置。

如果findLastBinaryOne(index)的返回是n 且$n > 1$，在BIT中，这个位置的值等于x中这个位置的值加上BIT[index - 2**0]， BIT[index - 2 ** 1] … BIT[index - 2 ** (n - 2)]

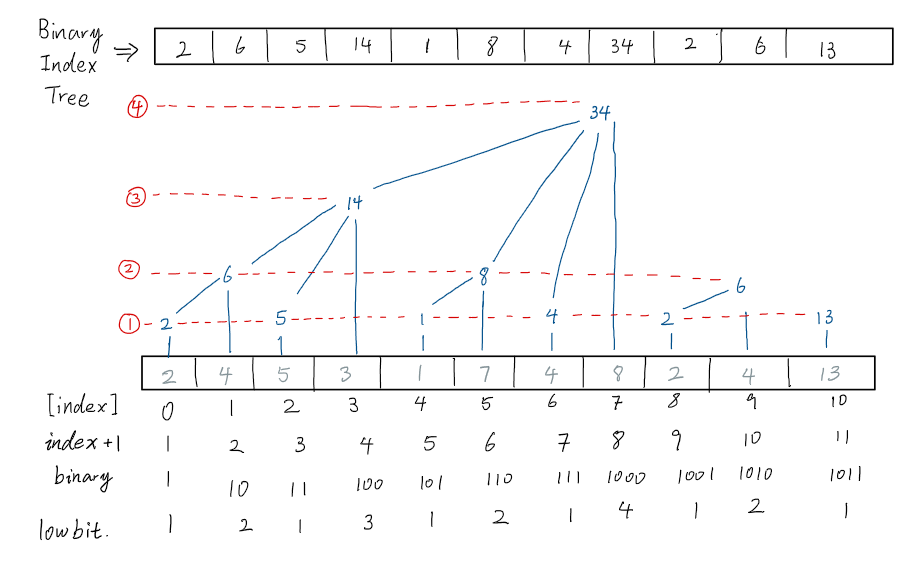
假设我们计算BIT中一个位置的值（假设BIT树中前面的值都是正确的），我们可以这样写：

private int getBITVal(int i){
    //return the BIT value on i
    int sum = 0;
    int power = 0;
    int pos = i;
    int maxPower = this.findLastBinaryOne(i);
    while (i >= 0 && power < maxPower){
        if (power == 0){sum += this.val[i];}
        else{sum += this.tree[i];}
        i = pos;
        i -= (int) Math.pow(2, power);
        power ++;
    }
    return sum;
}

因为每次我们调用getBITVal函数的时候我们都假设BIT中左侧的地方已经被初始好了，当我们初始化整个BIT时，我们需要从左到右的计算数组中每一个位置的 BIT值

private void initializeBIT(){
    for (int i = 0; i < this.tree.length; i ++){this.tree[i] = this.getBITVal(i);}
}

考虑到每次调用getBITVal都需要$O(\log{n})$的时间复杂度，我们初始化整个BIT数组的时间复杂度会是$O(n \log{n})$。虽然高于传统方法的$O(n)$，但是考虑到一般初始化代码只会执行一次，这个时间复杂度是可以接受的

Get Sum from BIT

我们现在已经有了BIT，那么我们怎么使用它查询一个区间内的元素和呢？首先，我们先看如何通过BIT查询 0 - index的区间和。观察上面的图，我们不难发现，一个BIT并不是单独的一棵树，而是很多棵子树所构成的，每个子树的根节点代表它所有叶子节点的和。那么，如果我们要计算0 - index的区间和的话，我们只需要找到index的二进制，然后每次去掉其中排在最后的一个1即可。（对应的是index前的根节点）

例子：如果我们需要计算 0 - 6之间的区间和，我们要 …

1. binary (6 + 1) = 1011
2. sum = tree[1011] + tree[1010] + tree[1000] = tree[7] + tree[6] + tree[4]

用java代码表示，就是这样：

public int getSum(int endIndex){
    int sum = 0;
    if(endIndex == 0){return this.tree[0];}
    while(endIndex > 0){
        sum += this.tree[endIndex];
        endIndex -= (int) Math.pow(2, this.findLastBinaryOne(endIndex) - 1);
    }
    return sum;
}

注意到循环的执行次数最大为索引二进制数的长度，也就是$\log_2{\text{index}}$，这说明调用一次getSum函数只会有$O(\log{n})$的时间复杂度

有了从0到index的区间和，我们就可以很方便的计算出任意两个索引之间的区间和（因为同是求区间和，这里直接重载了之前的getSum函数）

public int getSum(int startIndex, int endIndex){
    return this.getSum(endIndex) - this.getSum(startIndex);
}

Update BIT Tree

前文提到过BIT最大的优势是在保证快速求出区间和的同时可以快速进行数据结构的更新，接下来我们看看BIT是怎么进行数据结构的更新的：

如果我们想要更改this.val中的数据，我们必须更新其对应的树结构。因为BIT中兄弟节点是互不影响的，我们只用更新被更新索引所在的BIT树的所有父节点就可以了。

因为树的高度取决于索引二进制的长度，总共需要更新的节点数量的上限为$O(\log{n})$，用Java代码可以这样写：

private ArrayList<Integer> getParents(int index){
    ArrayList<Integer> parents = new ArrayList<Integer>();
    while (true){
        int currStep = (int) Math.pow(2, this.findLastBinaryOne(index) - 1);
        index += currStep;
        if(index > this.tree.length){break;}
        parents.add(index);
    }
    return parents;
}

public void updatePoint(int index, int newVal){
    this.tree[index] -= this.val[index] - newVal;
    this.val[index] = newVal;
    ArrayList<Integer> parents = this.getParents(index);
    for (int i = 0; i < parents.size(); i ++){
        this.tree[parents.get(i)] = this.getBITVal(parents.get(i));
    }
}

（上面的代码因为每个父节点更新都调用了一次getBITval函数，实际上的时间复杂度是$O((\log{n})^2)$， 通过修改实现方式，我们可以达到 $O(\log{n})$ 的时间复杂度）

练习

• USACO 2017 Feb Problem 3. Why Did the Cow Cross the Road III
• USACO 2017 Jan Problem 1. Balanced Photo
• USACO 2020 US Open Contest, Gold Problem 1. Haircut

更多

二维 Binary Index Tree

评论区