排序算法

Algorithm Notes

---

Mark Chen | 22 Feb 2021

报告错误

如果你发现该网页中存在错误/显示异常，可以从以下两种方式向我们报告错误，我们会尽快修复：

1. 使用 CS Club 网站错误 为主题，附上错误截图或描述及网址后发送邮件到 286988023@qq.com
2. 在我们的网站代码仓库中创建一个 issue 并在 issue 中描述问题 点击链接前往Github仓库

你使用哪种语言？我们会根据你选择的语言显示对应的代码示例

Python

Java

前置条件

在学习这个知识点前，你应该先学习……

• 数据结构：列表 Array (List) and ArrayList
• 理论基础：时间复杂度 Time Complexity
• 算法：递归 Recursion
• 算法：分治算法 Divide and Conquer

排序算法入门

大部分人的算法入门都是通过各种排序算法开始的，通过学习排序算法，我们可以清楚的比较算法之间的优劣和不同的特性来体会为什么我们需要算法，以及算法能够如何提升我们程序的效率。

在开始之前，先给一个非常实用的算法可视化网站 - VisualAlgo！如果你有没理解的算法，可以在这个网站上选择对应的算法观看它的可视化来辅助理解。

当然，如果你有问题在尝试自己寻找答案后还没搞懂，欢迎来找助教们问问题 点击这里找助教 （提问前可以先看看这篇文章：提问的方法）

排序算法性能对比

插入排序 Insertion Sort

时间复杂度 $O(n^2)$

《算法导论》书本 Page 16 - 20

我们将序列( 比如 Array/ArrayList )中的元素从**逻辑上分成两个部分**，左边是已经排好序的 (sorted)，右边是还没有排好序的 (unsorted)。

插入排序的思路就是**不断地将 unsorted 中的第一个元素，插入到左边 sorted 部分的相应位置**。这样的话，每插入一次，sorted 部分的s长度就会增加一。不断重复插入这个动作，直到整个数组排好序为止

理解要点

1. 还没开始插入的时候，sorted 部分已经有一个元素，也就是序列中的第一个元素。因为只有一个元素的序列一定是 sorted 的
2. 每一次插入，sorted 的部分一定会多加一个元素
3. 综合上述两点，n 个元素的序列，一定会进行 n-1 次操作。比如 6 个元素的序列，需要5次插入；100个元素的序列，需要99次插入。**这 n-1 次操作可以保证将这个序列排好序** 。

在实现插入这个操作的时候要注意，我们说的插入是**逻辑上的插入**，并不一定是实际操作上的插入。我们需要通过移动序列中的元素来达到插入的效果。如果一个靠后的元素要插入到前面的位置，那么意味着在它原来位置和插入位置之间的元素，需要全体往后挪一格，这样才能腾出插入位置。

伪代码

代码范例

def insertionSort(arr: list) -> list:
    for i in range(2, len(arr)):
        key = arr[i]
        j = i - 1
        while (j > 0 and arr[j] > key):
            arr[j + 1] = arr[j]
            j -= 1
        a[j + 1] = key
    return arr


public static ArrayList<Integer> insertionSort(<ArrayListInteger> arr){
  for (int i = 1; i < arr.size(); i ++){
      int key = arr.get(i);
      int j = i - 1;
      while (j > 0 && arr.get(j) > key){
          arr.set(j + 1, arr.get(j));
          j -= 1;
      }
      arr.set(j + 1, key);
  }
  return arr;
}

选择排序 Selection Sort

时间复杂度 $O(n^2)$

我们将序列( 比如 Array/ArrayList )中的元素从**逻辑上分成两个部分**，左边是已经排好序的 (sorted)，右边是还没有排好序的 (unsorted)。选择排序的思路就是**选择 unsorted 中的最小元素， 和 unsorted 中的第一个元素进行交换**。

伪代码

代码实现

def selectionSort(arr: list) -> list:
    for i in range(len(arr)):
        minValue = float("inf")
        minIndex = -1
        for j in range(i, len(arr)):
            if arr[j] < miValue:
                minValue = arr[j]
                minIndex = j
        
        # Python's Special Method to swap value of variables
        arr[i], arr[minIndex] = arr[minIndex], arr[i]


public static ArrayList<Integer> selectionSort(ArrayList<Integer> arr){
  for (int i = 0; i < arr.size(); i ++){
      int minValue = Integer.MAX_VALUE;
      int minIndex = -1;
      for (int j = i; j < arr.size(); j ++){
          if (arr.get(j) < minValue){
              minValue = arr.get(j);
              minIndex = j;
          }
      }
      int temp = arr.get(i);
      arr.set(i, minValue);
      arr.set(minIndex, temp);
  }
  return arr;
}

>>> a = 1
>>> b = 2
>>> a, b = b, a
>>> a
2
>>> b
1

冒泡排序 Bubble Sort

时间复杂度 $O(n^2)$

《算法导论》书本 Page 40

每次比较两个两两相邻的元素，如果较大的数字在前，将两个数字交换一下

伪代码

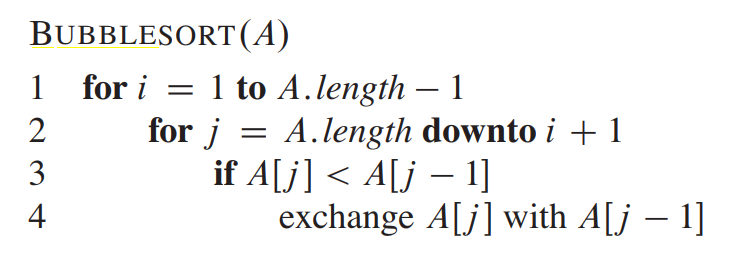
冒泡排序时间复杂度比较高，但是表现比较稳定，实现简单，所以是一种比较常见的排序算法

算法实现

def bubbleSort(arr: list) -> list:
    for i in range(0, len(arr) - 1):
        for j in range(len(arr), i + 1, -1):
            if arr[j] > arr[j - 1]:
                arr[j], arr[j - 1] = arr[j - 1], arr[j]
    return arr


public static ArrayList<Integer> bubbleSort(ArrayList<Integer> arr){
    for (int i = 0; i < arr.size() - 1; i ++){
        for (int j = arr.size(); j > i + 1; j --){
            if (arr.get(j) > arr.get(j - 1)){
                int temp = arr.get(j);
                arr.set(j, arr.get(j - 1));
                arr.set(j - 1, temp);
            }
        }
    }
    return arr;
}

归并排序 Merge Sort

时间复杂度 $O(n\log{n})$

《算法导论》书本 Page 30 - 34

每次我们将一个给定的序列分成两份，并且用归并排序递归的对分出来的两个子序列分别排序，直到子序列长度为1为止。接着开始合并。因为两侧的子序列都已经被排好序了，每次只用对比子序列最左侧的两个数，取较小的数字到结果的序列中。

VisualAlgo Sort 动画演示

伪代码

代码实现

def merge(a, b, m, e):
    l = a[b : m + 1]
    r = a[m + 1 : e + 1]
    k = b
    i = 0
    j = 0
    while i < len(l) and j < len(r):
        if l[i] < r[j]:
            a[k] = l[i]
            i += 1
        else:
            a[k] = r[j]
            j += 1
        k += 1
    while i < len(l):
        a[k] = l[i]
        i += 1
        k += 1
    while j < len(r):
        a[k] = r[j]
        j += 1
        k += 1
    return a


def mergesort(a, b, e):
    if b < e:
        m = (b + e) // 2
        mergesort(a, b, m)
        mergesort(a, m + 1, e)
        merge(a, b, m, e)
        return a


 public static void mergeSort(ArrayList<Integer> arr, int left, int right){
     if (right <= left){ return; }
     int middle = (left + right) / 2;
     // Recursion Case
     mergeSort(arr, left, middle);
     mergeSort(arr, middle + 1, right);

     //Merge the result of sorted sub-arrays
     int[] leftArr = new int[middle - left];
     int[] rightArr = new int[right - middle - 1];
     for (int i = left; i <= middle; i ++){
         // The Index Here will be tricky
         leftArr[i - left] = arr.get(i);
     }
     for (int i = middle + 1; i <= right; i ++){
         rightArr[i - middle - 1] = arr.get(i);
     }
     int leftArrHead = 0, rightArrHead = 0, originArrHead = left;
     while (leftArrHead < leftArr.length && rightArrHead < rightArr.length){
         if (leftArr[leftArrHead] < rightArr[rightArrHead]){
             arr.set(originArrHead, leftArr[leftArrHead]);
             leftArrHead += 1;
         }
         else{
             arr.set(originArrHead, rightArr[rightArrHead]);
             rightArrHead += 1;
         }
         originArrHead += 1;
     }
     // Deal with the Remaining Elements in Left / Right Array.
     while (leftArrHead < leftArr.length){
         arr.set(originArrHead, leftArr[leftArrHead]);
         leftArrHead += 1; originArrHead += 1;
     }
     while (rightArrHead < rightArr.length){
         arr.set(originArrHead, rightArr[rightArrHead]);
         rightArrHead += 1; originArrHead += 1;
     }
 }

快速排序 Quick Sort

时间复杂度 $O(n\log{n})$

《算法导论》Page 170 - 180

伪代码

代码实现

    
def quick_sort(array,begin,end):
    if begin<end:
        mid = partition(array, begin, end)
        quick_sort(array,begin,mid-1)
        quick_sort(array,mid,end)

def partition(array,low,high):
    key = array[low]
    while low < high:
        while low < high and array[high] >= key:
            high -= 1
        if low < high:
            array[low] = array[high]

        while low < high and array[low] < key:
            low += 1
        if low < high:
            array[high] = array[low]
    array[low] = key
    return low
    
    
  public static void quickSort(ArrayList<Integer> arr, int left, int right){
  if (left < right) {
      int mid = Sort.quickPartition(arr, left, right);
      quickSort(arr, left, mid - 1);
      quickSort(arr, mid, right);
  }
}

public static int quickPartition(ArrayList<Integer> arr, int left, int right){
  int pivot = arr.get(left);
  while (left < right){
      while (left < right && arr.get(right) >= pivot){
          right -= 1;
      }
      if (left < right){
          arr.set(left, arr.get(right));
      }

      while (left < right && arr.get(left) < pivot){
          left += 1;
      }
      if (left < right){
          arr.set(right, arr.get(left));
      }
  }
  arr.set(left, pivot);
  return left;
}
    

评论区