We Learn   We Create   We Share

初学者指南
笔记
竞赛
关于我们
页面搜索

目录

二维前缀和 2D Prefix Sum

Algorithm Notes

Mark Chen | 26 May 2021

前提条件

应用场景

在一些算法题中，我们需要快速求出二维数组内一个特定区域的所有值的和。这种时候，如果我们每次都使用遍历的方法求和，每次查询的时间复杂度是 $O(n^2)$，对于铜组以上的算法题来说这种时间复杂度一般是不可接受的。

二维前缀和就是专门用于解决这个问题的一种数据结构。二位前缀和会在初始化的时候使用 $O(n^2)$ 的时间复杂度建立一张二维数组从当前位置到 $[0][0]$ 的所有数字的和的表格。当初始化完成后，每次 $query$ 操作只需要 $O(1)$ 的时间复杂度就可以完成。

注意这种数据结构并不适合在二维数组需要大量更新的情况下使用，因为二位前缀和数组每次更新需要重新构造从更新位置开始的所有表格。每次更改的时间复杂度是 $O(n^2)$

原理

二位前缀和数据结构会在内部维护两张表格 $T$ 和 $S$。$S[y][x]$ 处存储的值等于 $T$ 中所有 $(0, 0)$ 到 $(x, y)$ 的位置的值之和。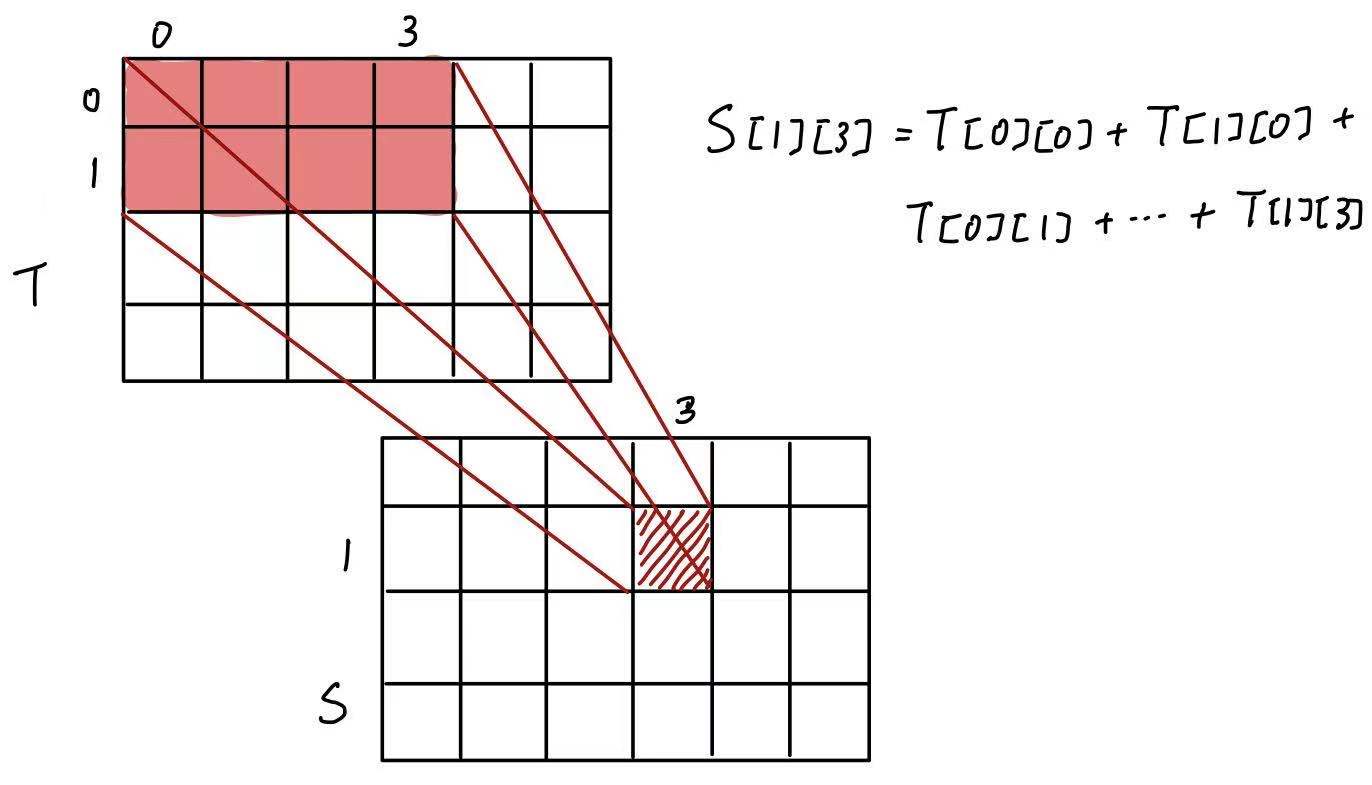04eed1e3dc29fba7bb34be79cb605bb

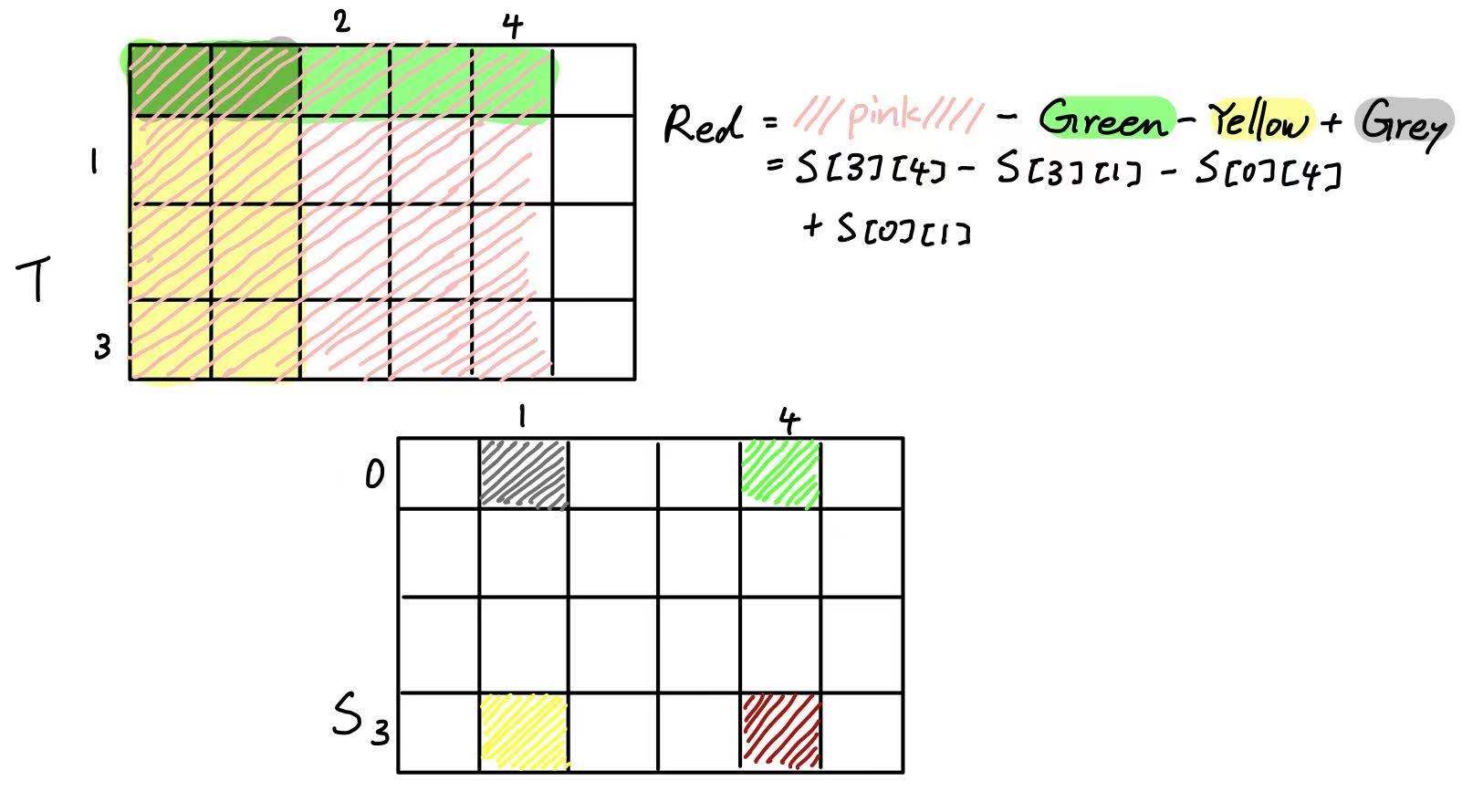
当我们想查询两个点 $(x_1, y_1)$ 与 $(x_2, y_2)$ 构成的矩形内部所有数字的和时，我们可以这样计算：

84e8f29abc499e4d5bbd3e209144ab5

表格 $S$ 可以使用下面这个公式遍历的方法生成

\[S[x][y] = S[x - 1][y] - S[x - 1][y - 1] + S[x][y - 1] + T[x][y]\]

注意上面 $S$ 中内容的运算顺序，对于 Java 等数值类型有最大值的语言，这样的顺序可以一定程度上的避免出现 Overflow 问题

实现

下面是基于 Java 范型 (Generic Type) 实现的一个二维数组。它可以存储任意数字类型的二维数组，但是查询时返回的内容总是 double 类型。


import java.util.ArrayList;

public class PrefixSum2D<T extends Number> {
    public static void main(String[] args) {
        Integer[][] arr = new Integer[][] {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
        PrefixSum2D<Integer> test = new PrefixSum2D<Integer>(arr);
        System.out.println(test.query2DSum(1, 0, 2, 2));
    }

    private ArrayList<ArrayList<T>> valueTable = new ArrayList<ArrayList<T>>();
    private ArrayList<ArrayList<Double>> sumTable = new ArrayList<ArrayList<Double>>();

    public PrefixSum2D(T[][] valueTable){
        for (int i = 0; i < valueTable.length; i ++){
            if (i == this.valueTable.size()){ this.valueTable.add(new ArrayList<T>()); }
            for (int j = 0; j < valueTable[0].length; j ++){
                this.valueTable.get(i).add(valueTable[i][j]);
            }
        }
        this.initializeTable(valueTable[0].length, valueTable.length);
        this.constructTable(0, 0);
    }

    public double query2DSum(int x1, int y1, int x2, int y2){
        /*
            Query the sum of all numbers in range ([x1, x2], [y1, y2]) with Time Complexity O(1)
                (x1, y1) ------------- (x2, y1)
                    |                     |
                    |                     |
                (x1, y2) ------------- (x2, y2)
        */
        x1 -= 1; y1 -= 1;
        if (x1 < 0 && y1 < 0){ return this.getTable(x2, y2); }
        else if (x1 < 0) { return this.getTable(x2, y2) - this.getTable(x2, y1); }
        else if (y1 < 0) { return this.getTable(x2, y2) - this.getTable(x1, y2); }
        else { return this.getTable(x2, y2) - this.getTable(x1, y2) - this.getTable(x2, y1) + this.getTable(x1, y1); }
    }

    public void slowUpdateTable(int x, int y, T value){
        /* Update 2D Prefix Sum Table with O(n^2) complexity */
        this.valueTable.get(y).set(x, value);
        this.constructTable(x, y);
    }

    private void initializeTable(int x, int y){
        /* Initialize the SumTable with size x * y and filled with null */
        for (int i = 0; i < y; i ++){
            this.sumTable.add(new ArrayList<Double>());
            for (int j = 0; j < x; j ++){
                this.sumTable.get(this.sumTable.size() - 1).add(null);
            }
        }
    }

    private void constructTable(int x, int y){
        /*
        Construct Table from T[y][x]
        Time Complexity: O(n^2), slow, don't call this method frequently
         */
        for (int i = y; i < this.sumTable.size(); i ++){
            for ( int j = x; j < this.sumTable.get(0).size(); j ++){
                double value = this.valueTable.get(i).get(j).doubleValue();
                if (i - 1 >= 0){ value += this.sumTable.get(i - 1).get(j); }
                if (i - 1 >= 0 && j - 1 >= 0){ value -= this.sumTable.get(i - 1).get(j - 1); }
                if (j - 1 >= 0){ value += this.sumTable.get(i).get(j - 1); }
                this.sumTable.get(i).set(j, value);
            }
        }
    }

    private double getTable(int x, int y){ return this.sumTable.get(y).get(x); }
}

评论区