We Learn   We Create   We Share

初学者指南
笔记
竞赛
关于我们
页面搜索

目录

线段树 Segment Tree

Algorithm Notes

Mark Chen | 21 May 2021

前提条件

使用场景

线段树的应用场景与二进制索引树相似，当我们需要多次查询数组子区间的特性/数据并同时高效修改数组内容的时候，我们可以使用线段树。

线段树并不是一种单一的数据结构 - 它代表了一类具有相同思想方法的数据结构 - 通过二叉树做到区间内容的高效查询，这里的内容可以是区间最大/最小值，区间和，等等 。

数据结构

线段树是一个二叉树，线段树中的每一个节点代表序列中的一个区间。假设对于 长度为 $N$ 的 array $A$，我们有对应的线段树 $T$，那么……

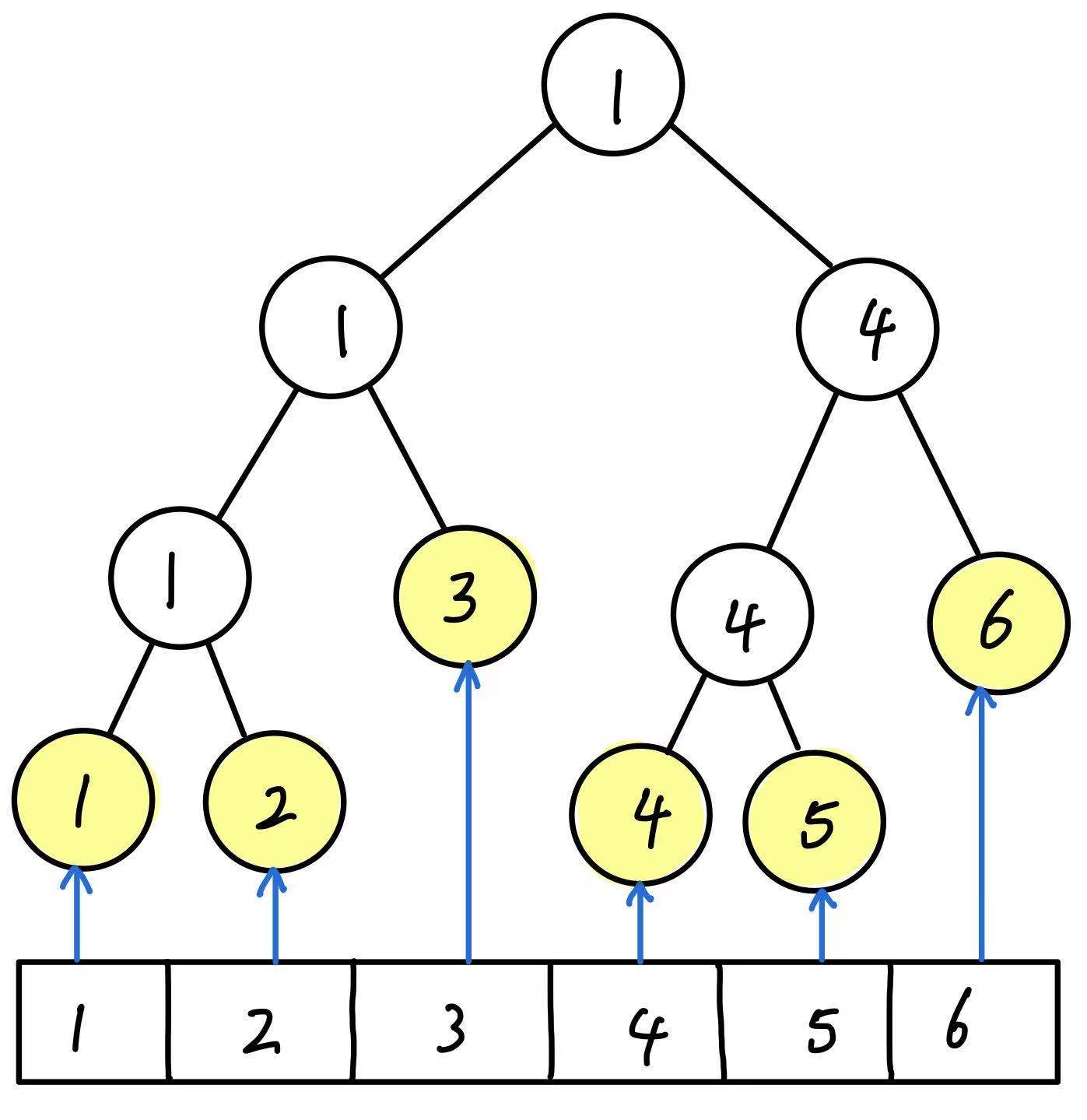
c8def3486964f5c15f15ac41ecacbc0

在一个线段树中，所有的叶子节点一定代表原数组中的一个值

注意线段树不一定是满二叉树

时间复杂度

初始化复杂度 - $O(n)$

对于一个长度为 $n$ 的 array，对应的线段树中最多一共有 $2n + 1$ 个节点。每个节点的初始化都是 $O(1)$ 的时间复杂度，所以线段树的初始化复杂度是 $O(n)$。

更新复杂度 - $O(\log{n})$

对于一个长度为 $n$ 的 array，每次修改一个单一的值需要修改这个节点的所有父节点与“祖先节点”（例如父节点的父节点，父节点的父节点的父节点……）。对于一颗线段树，最多有 $\log_2{n}$ 的高度，所以更新一次线段树的值的时间复杂度是 $O(\log_2{n}) = O(\log{n})$

查询复杂度 - $O(\log{n})$

查询节点数量最多的情况出现于查询 $[l, l]$ 时，这时候我们需要从根节点一路递归的遍历到叶子节点，一共遍历 $O(\log{n})$ 个节点。所以查询区间的时间复杂度是 $O(\log{n})$

Java实现

一个线段树有三个主要的方法：

下面，我们会实现一个基于 范型 (Generic Type) 的最小线段树。对于任意实现了 Comparable 接口的类型 T 的 ArrayList<T>，我们都可以使用这个线段树来求出区间 $[l, r]$ 中的最小对象 $T$。

Helper Functions

在正式实现线段树前，我们先写一些后面可以用到的 Helper Functions。

public class SegmentTree <T extends Comparable<T>>{
    private ArrayList<T> tree;
    private T[] value;
    
	private int getLChild(int index){ return index * 2 + 1; }
    private int getRChild(int index){ return index * 2 + 2; }
    private T genericMin(T o1, T o2){
        if (o1.compareTo(o2) > 0){ return o2; }
        return o1;
    }
    private int inInterval(int l1, int r1, int l2, int r2){
        if (r2 < l1 || l2 > r1){ return 0; }        // Intervals do not have any intersection
        else if (l2 >= l1 && r2 <= r1){ return 1; } // Interval 2 complete in Interval 1
        else{ return 2; }                           // Interval 2 partially intersect with Interval 1
    }
}

注意我们的 tree 属性使用的是 ArrayList 而不是 array

这是因为 Java 中不能创造 Generic Type Array

Construct Segment Tree

我们使用递归的方法来构建线段树 - 根节点的范围是 $[0, arr.length - 1]$，计算出中间的节点 $mid = (arr.length - 1) / 2$，左节点的范围就是 $[0, mid]$，右节点的范围是 $[mid + 1, arr.length - 1]$。

当节点的范围是 $[l, r]$ 且 $l = r$ 时，节点的值就是 Array 中对应元素的值 - 此时这个节点时叶子节点。

public SegmentTree(T[] values){
    this.tree = new ArrayList<>(Collections.nCopies(values.length * 2 + 1, null));
    this.value = values;
    this.constructTree(0, 0, values.length - 1);
}

private void constructTree(int node, int l, int r) {
    if (l == r) {
        tree.set(node, value[l]);
    } else {
        int mid = (l + r) / 2;
        this.constructTree(this.getLChild(node), l, mid);
        this.constructTree(this.getRChild(node), mid + 1, r);
        tree.set(node, this.genericMin(tree.get(this.getLChild(node)), tree.get(this.getRChild(node))));
    }
}

Update Segment Tree

类似的，我们在更新 Segment Tree 时也使用递归的方法更新 - 如果要修改的 index 在当前节点的范围内，我们就递归的修改下一层，最后再 bottom-up 的更新整条路径上的 $O(\log{n})$ 个节点

public void updateTree(int index, T val){
    this.updateTree(0, 0, this.value.length - 1, index, val);
}

private void updateTree(int node, int l, int r, int index, T val){
    if (l == r){
        this.tree.set(node, val);
        this.value[l] = val;
    }
    else{
        int mid = (l + r) / 2;
        if (l <= index && index <= mid){ this.updateTree(this.getLChild(node), l, mid, index, val); }
        else{ this.updateTree(this.getRChild(node), mid + 1, r, index, val); }
        this.tree.set(node, this.genericMin(this.tree.get(this.getLChild(node)), this.tree.get(this.getRChild(node))));
    }
}

Query Interval Minimum

在查询线段树中的区间最小值时，我们把所有情况分为三种：

对这三种情况，我们采取不同的动作

情况 操作
节点区间完全在查询区间内 返回当前节点的值
节点区间部分在查询区间内 继续向下递归，返回左节点与右节点返回值的较小值
节点区间完全不在查询区间内 返回 null 
public T queryMin(int l, int r){
    return queryMin(0, 0, this.value.length - 1, l, r);
}

private T queryMin(int node, int start, int end, int l, int r){
    if (this.inInterval(l, r, start, end) == 0){ return null; }
    else if (this.inInterval(l, r, start, end) == 1){ return this.tree.get(node); }
    int mid = (start + end) / 2;
    T leftInterval = this.queryMin(this.getLChild(node), start, mid, l, r);
    T rightInterval = this.queryMin(this.getRChild(node), mid + 1, end, l, r);
    if (leftInterval == null){ return rightInterval; }
    else if (rightInterval == null){ return leftInterval; }
    else{ return this.genericMin(leftInterval, rightInterval); }
}

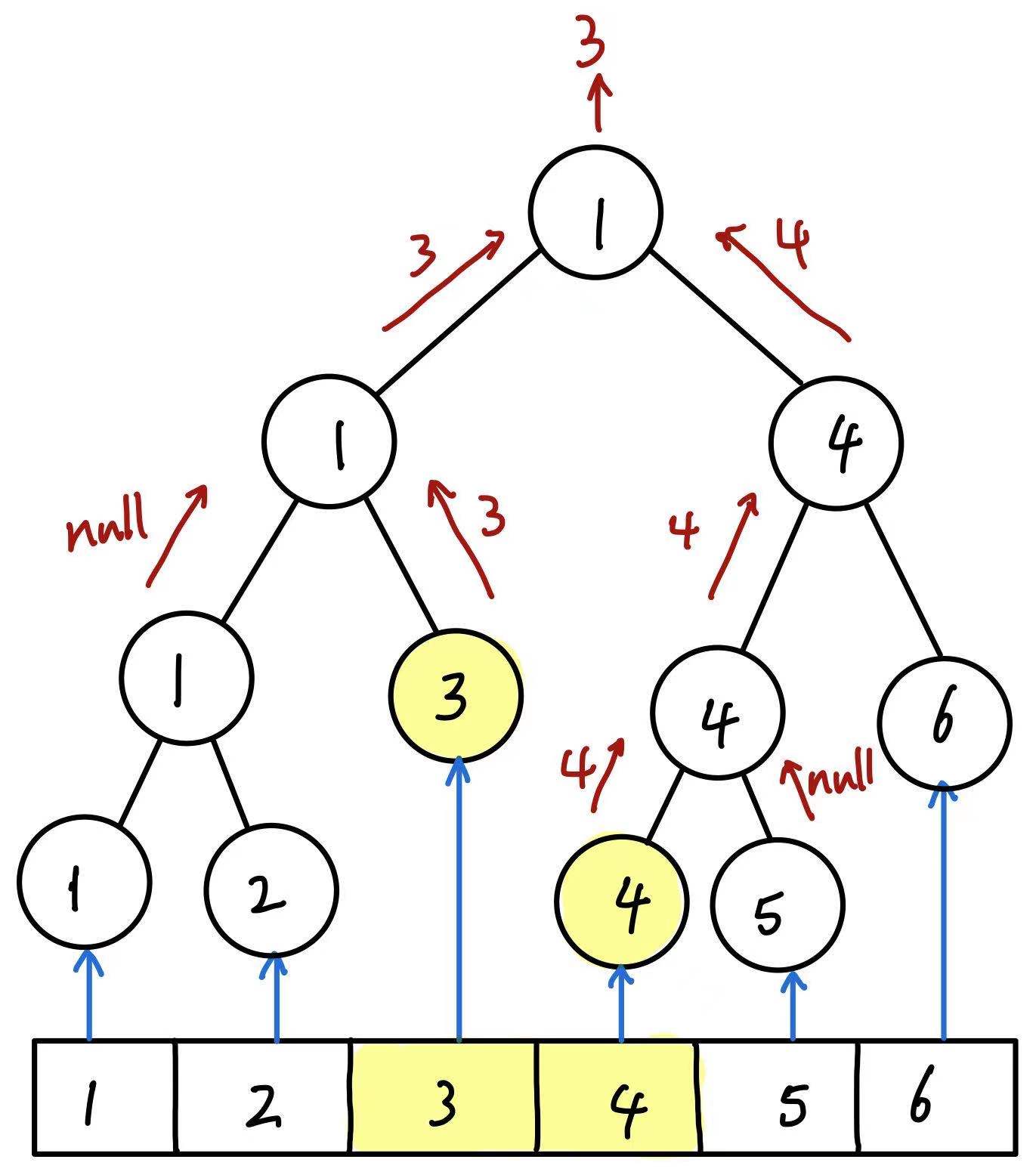
对于基于数组

Integer[]{1, 2, 3, 4, 5, 6}

的线段树，我们执行 queryMin(2, 3) 时函数的递归情况如下

fb5b1012c2c20d4f2ab433ad800d475

Click to see Java Full Code

 
        
 /* Segment Tree, Java */

import java.util.*;

public class SegmentTree <T extends Comparable<T>>{

    public static void main(String[] args) {
        SegmentTree<Integer> test = new SegmentTree<>(new Integer[]{1, 2, 3, 4, 5, 6});
        System.out.println(test.dumpTree());
        // test.updateTree(0, 7);
        // System.out.println(test.dumpTree());
        System.out.println(test.queryMin(2, 5));
    }
    
    private ArrayList<T> tree;
    private T[] value;
    
    public SegmentTree(T[] values){
        this.tree = new ArrayList<>(Collections.nCopies(values.length * 2 + 1, null));
        this.value = values;
        this.constructTree(0, 0, values.length - 1);
    }
    
    public void updateTree(int index, T val){
        this.updateTree(0, 0, this.value.length - 1, index, val);
    }
    
    public T queryMin(int l, int r){
        return queryMin(0, 0, this.value.length - 1, l, r);
    }
    
    public ArrayList<T> dumpTree(){
        return this.tree;
    }
    
    private T queryMin(int node, int start, int end, int l, int r){
        if (this.inInterval(l, r, start, end) == 0){ return null; }
        else if (this.inInterval(l, r, start, end) == 1){ return this.tree.get(node); }
        int mid = (start + end) / 2;
        T leftInterval = this.queryMin(this.getLChild(node), start, mid, l, r);
        T rightInterval = this.queryMin(this.getRChild(node), mid + 1, end, l, r);
        if (leftInterval == null){ return rightInterval; }
        else if (rightInterval == null){ return leftInterval; }
        else{ return this.genericMin(leftInterval, rightInterval); }
    }
    
    private void updateTree(int node, int l, int r, int index, T val){
        if (l == r){
            this.tree.set(node, val);
            this.value[l] = val;
        }
        else{
            int mid = (l + r) / 2;
            if (l <= index && index <= mid){ this.updateTree(this.getLChild(node), l, mid, index, val); }
            else{ this.updateTree(this.getRChild(node), mid + 1, r, index, val); }
            this.tree.set(node, this.genericMin(this.tree.get(this.getLChild(node)), this.tree.get(this.getRChild(node))));
        }
    }
    
    private void constructTree(int node, int l, int r) {
        if (l == r) {
            tree.set(node, value[l]);
        } else {
            int mid = (l + r) / 2;
            this.constructTree(this.getLChild(node), l, mid);
            this.constructTree(this.getRChild(node), mid + 1, r);
            tree.set(node, this.genericMin(tree.get(this.getLChild(node)), tree.get(this.getRChild(node))));
        }
    }
    
    private int getLChild(int index){ return index * 2 + 1; }
    private int getRChild(int index){ return index * 2 + 2; }
    private T genericMin(T o1, T o2){
        if (o1.compareTo(o2) > 0){ return o2; }
        return o1;
    }
    private int inInterval(int l1, int r1, int l2, int r2){
        if (r2 < l1 || l2 > r1){ return 0; }        // Intervals do not have any intersection
        else if (l2 >= l1 && r2 <= r1){ return 1; } // Interval 2 complete in Interval 1
        else{ return 2; }                           // Interval 2 partially intersect with Interval 1
    }
}

问题练习

评论区