报告错误
如果你发现该网页中存在错误/显示异常,可以从以下两种方式向我们报告错误,我们会尽快修复:
- 使用 CS Club 网站错误 为主题,附上错误截图或描述及网址后发送邮件到 286988023@qq.com
- 在我们的网站代码仓库中创建一个 issue 并在 issue 中描述问题 点击链接前往Github仓库
6.1 Define Constraint Satisfaction Problems
A CSP contains three components - $X$, $D$ and $C$.
- $X$ is a set of variables
- $D$ is a set of domains, one for each variable.
- $C$ is a set of constraints that specify the allowable combination between variables.
Each constraint can be represent in two parameters - the $scope$ and the $relation$. The $scope$ define the variables that is related with this constraint. The $relation$ define the values that variables can take.
The $relation$ can be either an explicit list of all legal value tuple the variables can get or an abstract relation.
Example 1 (Abstract, Implicit Relation) : If the constraint is $x < y$. The formal way to represent constraint will be:
\[\langle scope:(x, y),\quad relation:\;\lt\rangle\]Example 2 (Explicit Relation): If we have $0 < x < 4$ and $0 < y < 3$, the constraint can be represented in this way:
\[\langle scope: (x, y),\quad relation: [(1, 1), (1, 2), \cdots, (3, 1), (3, 2)] \rangle\]
To solve the Constraint Satisfaction Problem (abbr. as CSP below), we need to define the solution and state space for CSP first. Each state of CSP is defined by an **assignment** of values to some or all of the variables.
An assignment that does NOT violate any constraint in $C$ is called a consistent assignment (or, legal assignment).
A Complete Assignment is an assignment where every variable in $X$ is assigned.
The Solution of CSP is both Complete Assignment and Consistent Assignment.
6.2 Why we need CSP
In the real world, many problems can be converted to CSP. As long as we have a legal CSP solver, we can generalize this solver to different problems with little difficulty. It will be easier to use a generalized CSP solver than design a custom solution using domain-specific knowledge.
6.3 Solving CSP
When we are finding the solution of CSP, once we find out that a partial assignment is not a solution, we can immediately discard further refinements of the partial assignment.
6.3.1 Types of Constraints in CSP
| Constraint Type | Explanation |
|---|---|
| Unary Constraint | Constraint that only contain one variable in the scope Example: $\langle (x), x\neq 2\rangle$ |
| Binary Constraint | Constraint that contains two variables in the scope Example: $\langle (x, y), x < y \rangle$ |
| k-ary Constraint | Constraint that contains $k$ variables in the scope Example: $\langle (x, y, z), \max(x, y, z) < 5 \rangle$ |
| Global Constraint | Constraint that involving all variables in $X$ Example: $Alldiff$ Constraint requires all variables in $X$ has different assigned value. |
Every finite-domain constraint can be converted to a set of binary constraints if enough auxiliary variables are introduced. Therefore, we can Transform every CSP into CSP with binary constraint only.
6.3.2 Constraint Propagation: Inference in CSP
A regular search algorithm can only do one thing: search. In CSP, the algorithm can search or do specific type of inference called constraint propagation in CSP. Using constraint to reduce the number of legal values of a variable, which, in turn reduce the legal values of another variable.
Constraint propagation can work during the search process or work as a pre-processing step.
The key idea of constraint propagation is the local consistency. If we see each variable in CSP as node, binary constraint as edge of graph, the local consistency is the consistency in a part of the whole constraint graph.
Basically, you can see local consistency as a set of pruning algorithms running on CSP. By cutting off domain of each variable, the workload for search algorithm is greatly reduced.
Node Consistency
Node Consistency Check tighten the unary domain using unary constraint
A single variable is node-consistent if all the values in the variable’s domain satisfy the variable’s unary constraints.
It is always possible to eliminate all the unary constraints in a CSP by running node consistency.
Arc Consistency
Arc Consistency Check tighten the unary domain using binary constraint
A variable in a CSP is arc-consistent if every value in its domain satisfies the variable’s binary constraints.
Formally speaking, $X_i$ is arc-consistent with respect to $X_j$ if for every value in $D_i$ there exist some value in $D_j$ such that the binary constraint between $X_i$ and $X_j$ is satisfied.

Note - iff stands for if and only if
AC3 is the most popular algorithm for arc consistency. To make every variable arc-consistent, the AC-3 algorithm maintains a queue of arcs to consider. Initially, the queue contains all the arcs in the CSP. AC-3 then pops off an arbitrary arc $(X_i, X_j)$ from the queue and makes $X_i$ arc-consistent with respect to $X_j$.
If this step makes the domain $D_i$ of variable $X_i$ unchanged, we will move forward to next arc.
If not, we add to the queue all arcs $(X_k, X_i)$ where $X_k$ is a neighbor of $X_i$. This is because the change of domain $D_i$ may lead to further reduction in the domain of $D_k$, even if we have previously considered $X_k$.
An arc-consistency CSP is equivalent to original CSP, but faster to search because its variables has smaller domains.
Path Consistency
Path Consistency Check tighten the binary constraints by using implicit constraints that are inferred by triples of variables
In Arc Consistency, we are using binary constraint to optimize the unary domain. For most of the cases, this works well and can directly find solution (every domain is restricted to only 1 value) or prove that there is no solution for CSP (at least one domain contains 0 valid value).
However, in some situation, the arc consistency has nothing to do with the unary domain using only binary constraint.
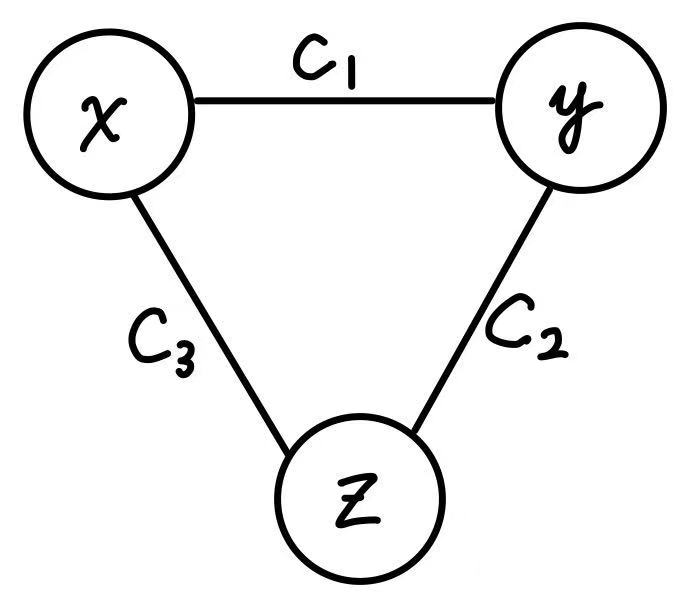
Example 3. A situation that arc consistency doesn’t work as expected
$X = {x, y, z}$
$D = {[Red, Blue], [Red, Blue], [Red, Blue]}$
$C = {\langle(x, y), x\neq y\rangle, \langle(z, y), z\neq y\rangle, \langle(x, z), x\neq z\rangle}$
If we are running arc consistency on this CSP, no domain will be changed. (When $x = Red$, $y = Blue$ is valid and vice versa). However, it is clear that this CSP will have no solution.
To solve this problem, we introduce the thought of Path Consistency.
Formal description of Path Consistency:
A two-variable set ${x_i, x_j}$ is path consistent with a third-variable ${x_k}$ if for every assignment ${x_i = a, x_j=b}$ that satisfy the constraint between $x_i$ and $x_j$, there exists a valid assignment to $x_k$ such that the constraint between $x_k$ and $x_i$, $x_k$ and $x_j$ is not violated.
$k$-Consistency
A generalized way to represent consistency of CSP is called $k$-consistency. A CSP is $k$-consistent if for any set of $k-1$ variables and for any consistent assignment to these variables, there always exist a consistent assignment to $k$th variable.
Node Consistency = 1-consistency, Arc Consistency = 2-consistency, Path Consistency = 3-consistency
A CSP is strongly k-consistent if it is $k$-consistent and is also $(k-1)$-consistent, $(k-2)$-consistent … all the way to $1$-consistent.