报告错误
如果你发现该网页中存在错误/显示异常,可以从以下两种方式向我们报告错误,我们会尽快修复:
- 使用 CS Club 网站错误 为主题,附上错误截图或描述及网址后发送邮件到 286988023@qq.com
- 在我们的网站代码仓库中创建一个 issue 并在 issue 中描述问题 点击链接前往Github仓库
1. 图论 Graph Theory
图论是将实际问题转化为由节点和边构成的图的一种数学模型。在之前的ACSL专题中,我们已经接触了一些图论的概念 - 例如树,环,节点 和 边。在这个专题里面,我们会重新系统性的学习图论相关知识。
1.1 图论基础
1.1.1 有向图与无向图
根据节点之间的关系,我们将所有的图分为两类,一种是有向图,一种是无向图。在有向图中,节点与节点之间的关系是单向的,也就是说,存在边 $A \rightarrow B$(下面略作边$AB$) 不一定意味着存在边 $B\rightarrow A$(下面略作边$BA$) 。在无向图中,边是没有方向的,也就是说边$AB$和边$BA$是等价的。
| 有向图 | 无向图 | |
|---|---|---|
| 图像 | 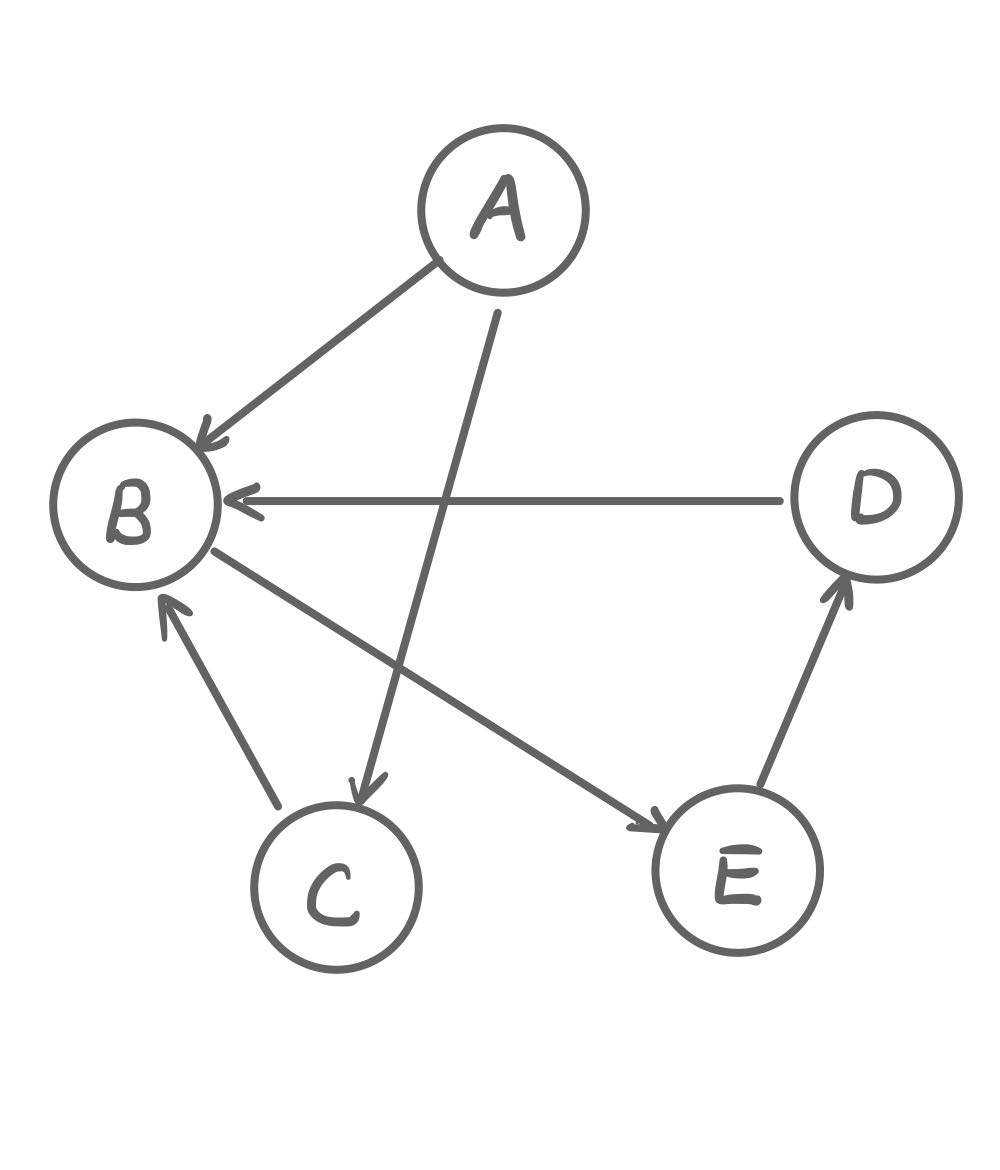 |
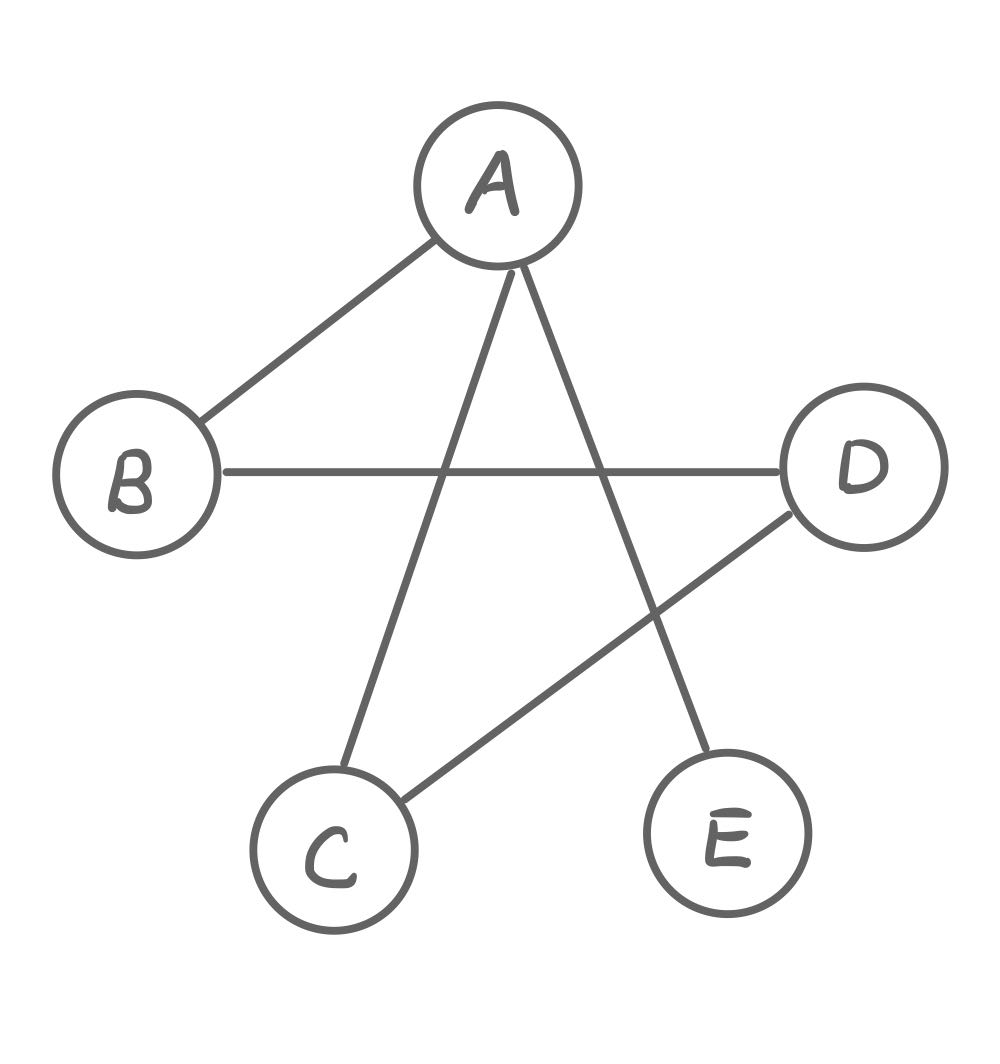 |
| 表示方法 | 有向图中,因为$AB$与$BA$ 表示的边不同,我们要分开表示。 \(V = \{A, B, C, D, E\}\\E=\{AB, AC, BE, CB, DB, ED\}\) |
无向图中,边没有方向,两个节点间的边我们直接表示为两个节点即可。 \(V = \{A, B, C, D, E\}\\E=\{AB, AC, AE, BD, CD\}\) |
| 边数 | 在有向图中,边数的取值范围:$E\in[V, V^2]$ | 在无向图中,边数的取值范围:$E\in[V, V(V-1)/2]$ |
1.1.2 路径的定义
在图中,路径可以用一串有顺序的节点来表达。例如在上图的无向图中,$DBAE$就是一条$D$到$E$的合法的路径。
Simple Path 的定义:一条 vertex 没有重复的 Path
Cycle 的定义:一条首尾节点相同的 Path
Tree 的定义:一个图如果没有环则成为 Tree,在一颗 Tree 中,任意两个节点之间只有一条 Path,树一定是 $G(V, V-1)$(边数为 $V-1$)
1.2 图的表达
1.2.1 节点与边
我们可以用一个 set 表示图$G$的节点$V$,用另一个 set 表示图$G$的边$E$,这两者共同定义了一个图。
1.2.2 邻接矩阵表示图
除了分别用节点与边表示一张图以外,我们还可以用邻接矩阵 (adjacency matrix) 表示一张图。对于一张图$G(V, E)$,我们可以用一个 $M = \lvert V\rvert\times\lvert V\rvert$ 的矩阵表示图中节点的关系 - 如果节点 $A$ 和 $B$ 之间有边相连,那么$M[A][B]$ 的值是 1,否则 $M[A][B]$ 的值是 0。
例如下面这张图

就可以用这样的一个矩阵表示:
\[M = \left[\begin{matrix} 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 \end{matrix}\right]\]使用这种方法表示矩阵,我们可以(相对)快速的计算两个节点之间长度为 $k$ 的路径数量。如果我们想知道节点$A$到$B$长度为$k$的路径数量,我们只需要查看$M^k[A][B]$的值即可。这里的$M^k$是邻接矩阵$M$的$k$次幂。
例如 - 在刚刚的有向图中,$A$ 到 $B$ 只有一条长度为2的路径,因为
\[M^2 = \left[\begin{matrix} 0 & 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0 & 0 \end{matrix}\right]\]而$M[A][B] = 1$。
点击查看矩阵乘法快速入门
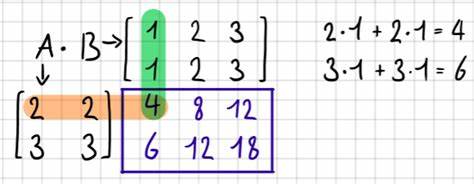
在这个专题中的邻接矩阵都一定是 $N\times N$ 的方阵,所以不用考虑矩阵乘法的维度问题。
如上图,对于一个给定的矩阵 $M$,如果我们想计算它的乘方,一种简便方法是将一个矩阵 $M$ 写在左侧,将相同的矩阵 $M$ 写在上方。这样我们计算 $M^2_{ij}$ 就只用计算 $M$ 的第 $i$ 行与 $M$ 的第 $j$ 列之间的点积结果就行了。
$$ M^2_{ij} = M_{i*}\cdot M_{*j} $$
1.2.3 邻接矩阵计算路径数量的原理
点击查看原理推导* (不感兴趣的可以跳过这个部分)
之前我们说过矩阵 $M$ 中 $M[A][B]$ 的值代表 $A$ 到 $B$ 的路径数量,那么矩阵中第 $B$ 列就代表了所有到达 $B$ 的路径,第 $A$ 行代表所有从 $A$ 出发的路径。
当我们计算矩阵 $M$ 的平方时,$M^2[A][B]$ 的值实际上是 $M$ 的第$A$行与第$B$列的点积结果。也就是可以这样表示(将$M[A][B]$ 写作 $M_{AB}$)
$$ M^2_{AB} = M_{A*}\cdot M_{*B} = M_{AA}M_{AB} + M_{AB}M_{BB} + M_{AC}M_{CB} + M_{AD}M_{DB} + M_{AE}M_{EB} $$
也就是说当我们在对矩阵进行平方运算的时候,我们实际上是在计算
$$\sum_{v\in V}{\left(A \text{到} v \text{长度为 1 的路径数量} \times v \text{到} B \text{长度为 1 的路径数量}\right)}$$
实际上这里的矩阵乘法只是批量的进行小学时学习的乘法原理进行计算而已……
1.3 考试题型与对应解法
1.3.1 找到节点间指定长度的路径数量
例子
In the following directed graph, find the number of different paths from vertex $A$ to vertex $C$ of length 2 or 4.
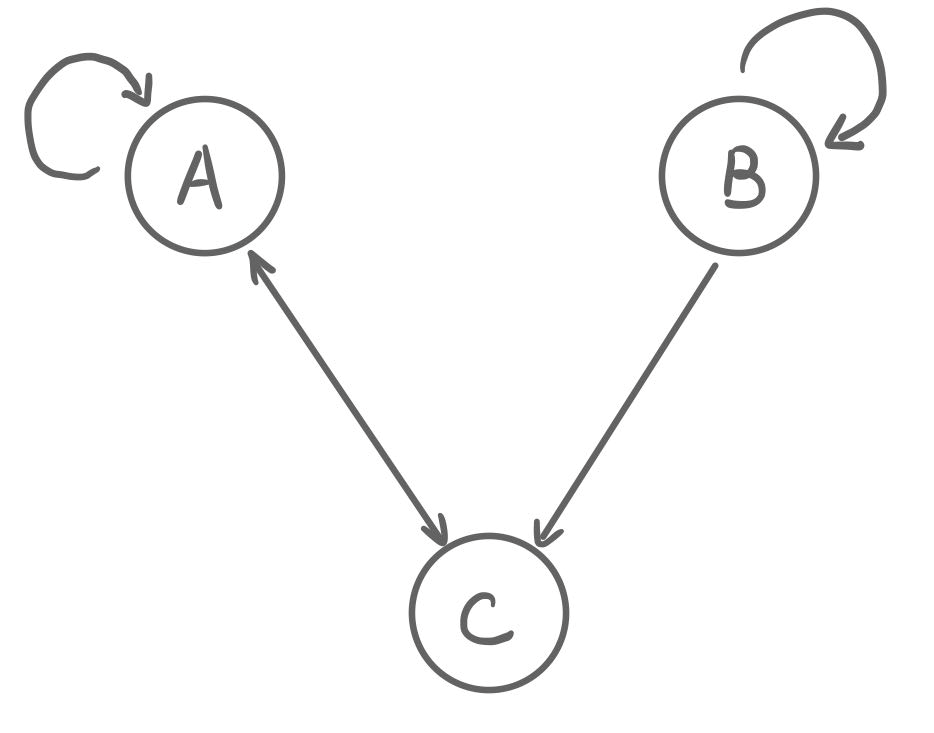
解答
找出题目中图的邻接矩阵 $M$,分别求出 $M^2$ 和 $M^4$ 的值。
\[M = \left[\begin{matrix} 1 & 0 & 1\\ 0 & 1 & 1\\ 1 & 0 & 0 \end{matrix}\right]\quad M^2 = \left[\begin{matrix} 2 & 0 & 1\\ 1 & 1 & 1\\ 1 & 0 & 1 \end{matrix}\right]\quad M^4 = \left[\begin{matrix} 5 & 0 & 3\\ 4 & 1 & 3\\ 3 & 0 & 2 \end{matrix}\right]\]所以我们可以知道 $A$ 到 $C$ 有1条长度为2的路径,3条长度为4的路径。
1.3.2 数 cycle 的数量
例子
How many cycles are in the following graph?
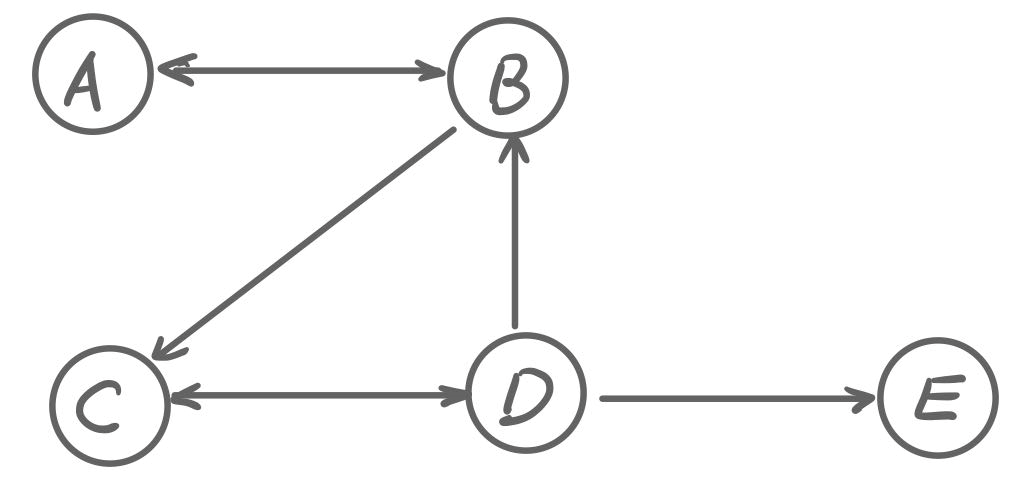
解答
这种题目适合用枚举法做
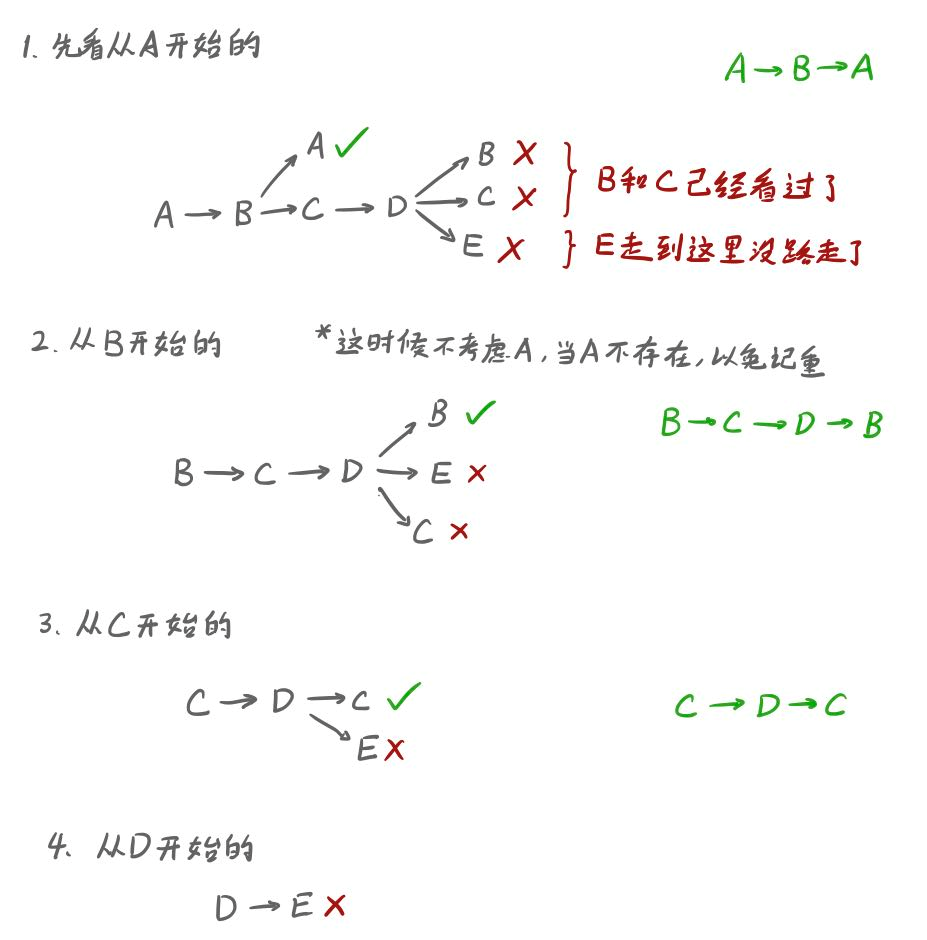
1.3.3 Adjacency Matrix 和 Graph 互相转化
例子
Given the adjacency matrix $M$, draw the directed graph.
\[M = \left[\begin{matrix} 0 & 1 & 0 & 1\\ 1 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 1 & 0 \end{matrix}\right]\]解答
这种题就按照上面介绍邻接矩阵的时候的规则(有边是1,没边是0)翻译就行了。这个矩阵是 $4\times 4$ 的,所以翻译出来的图一定有四个节点。
1.4 练习
Intermediate
题目
答案
Senior
题目
答案
2 汇编语言 Assembly Language
2.1 汇编语言简介
⾼级语⾔写出的程序通常会被编译器转换为 Assembly Language汇编语⾔,然后翻译为0和1组成的 机器语⾔。直到现在,理解Assembly Language仍然⾮常重要:
- 帮助你理解编译器的本质和它的限制
- 在某些情况下,直接使⽤Assembly Language可以满⾜运⾏速度或空间的限制 本章中,我们将会使用ACSL⾃⼰创造的Assembly Language,⽽不是真实运行在芯片上的汇编语言。
2.2 汇编语言运行方式
汇编语⾔从第⼀⾏顺序运⾏到最后⼀⾏END。其中可以有 分⽀命令branch instructions (如 BG, BE, BL, BU) 来实现循环等操作。每⼀次运算的结果会暂时储存在 accumulator (ACC) 这⼀特殊储存空间中。ACC默认为0。
2.2.1 汇编语言语法
汇编语言每一行遵循这样的格式
LABEL OPCODE LOC
LABEL部分类似于函数名称/变量名称。必须由字⺟开头,区分⼤⼩写。不新建函数/变量 时,可以空出。
OPCODE部分是实际的操作。解释⻅下面的表格,应该全部⼤写。OPCODE 是语⾔⾥的保留词 (reserved words) ,不可以⽤作 LABEL。
LOC部分引⽤⼀个LABEL或者⼀个immediate data,如常数 321。
2.2.2 汇编语言 OPCODE
运算指令
| OPCODE | 解释 |
|---|---|
| LOAD1 | 将语句中 LOC 位置的内容加载至 ACC 中,LOC 位置存储的内容不变 |
| STORE | 将当前 ACC 中的内容存放到 LOC 位置,ACC 中的内容不变 |
| READ2 | 将一个整数存入 LOC 位置中 |
| ADD1 2 | 将 LOC 位置中的内容 加到 ACC 中的内容上,LOC 位置存储的内容不变 |
| SUB1 2 | 将 ACC 中的内容 减去 LOC 位置中的内容,LOC 位置存储的内容不变 |
| MULT1 2 | 将 LOC 位置中的内容与 ACC 中的内容相乘,LOC 位置存储的内容不变 |
| DIV1 2 | LOC 位置的内容被 ACC 中的内容除了以后的结果整数部分存储到 ACC 中 |
分支指令
| OPCODE | 解释 |
|---|---|
| BG | 如果 ACC 的内容 $\gt 0$,跳转到 LOC 标记的位置 |
| BE | 如果 ACC 的内容 $= 0$,跳转到 LOC 标记的位置 |
| BL | 如果 ACC 的内容 $\lt 0$,跳转到 LOC 标记的位置 |
| BU | (无条件的)跳转到 LOC 标记的位置 |
其他指令
| OPCODE | 解释 |
|---|---|
| 打印 LOC 位置的内容 | |
| DC | 定义 LABEL 的值为 LOC 的内容,并且 LABEL 是一个常量 |
| END | 终止程序,执行这个 OPCODE 时,LOC 位置必须是空的 |
2.3 汇编语言例题
要能熟练看出题⽬的本质是顺序/循环/判断,改写为简单清晰的伪代码进⾏理解,快速得到答案。
例题:
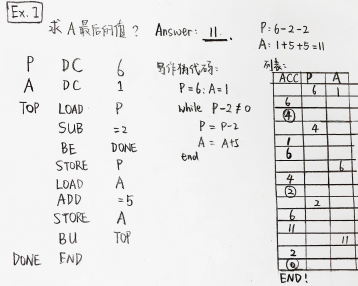
2.4 练习
题目
答案
3. 数字电路 Digital Electronics
3.1 简介
在之前的 ACSL 场次中,我们已经学习了 逻辑运算符 和 Boolean Algebra。这个专题使用逻辑电路实现特定的 Boolean Algebra 表达式并要求判断电路的输出状态。
一个电路由多个“元件”构成,每个原件执行一个简单的逻辑 - AND, OR, NOT, NOR, NAND 。通过组合这些原件的输入输出,我们可以使用它们表达布尔代数式。
3.2 数字电路介绍
| Name | Symbol | Boolean Expression | Truth Table |
|---|---|---|---|
| BUFFER |  |
$out = A$ | 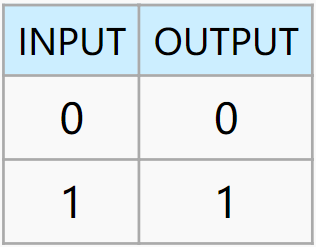 |
| NOT | 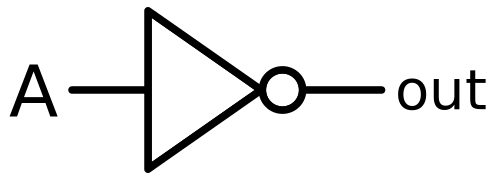 |
$out = \bar{A}$ | 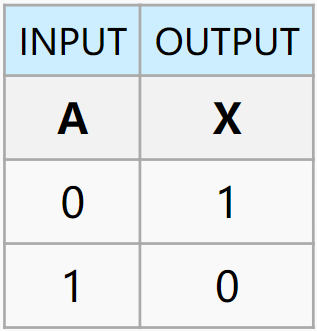 |
| AND |  |
$out = A \wedge B$ | 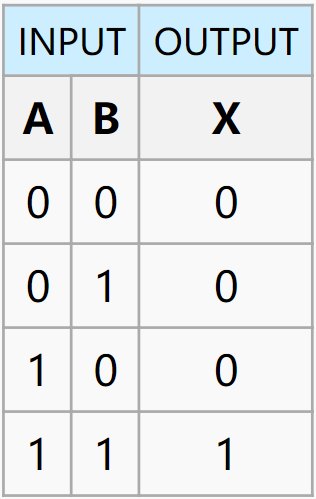 |
| NAND | 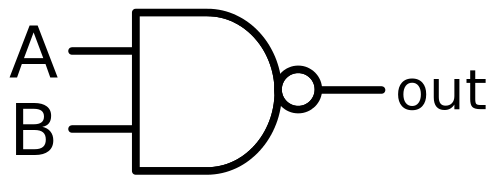 |
$out = \overline{A\wedge B}$ | 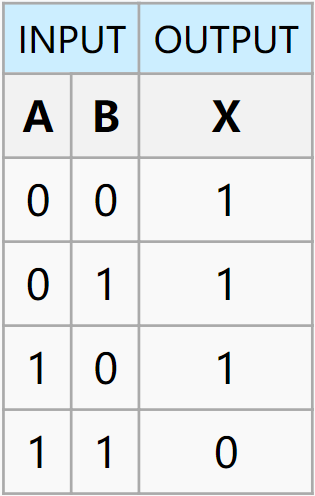 |
| OR |  |
$out = A\vee B$ | 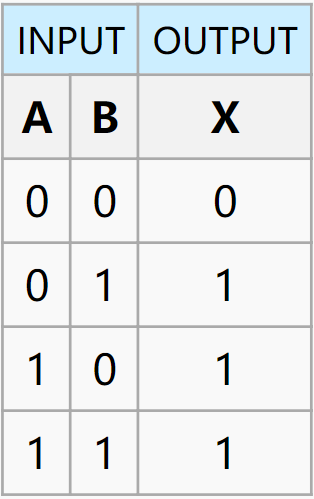 |
| NOR |  |
$out = \overline{A\vee B}$ | 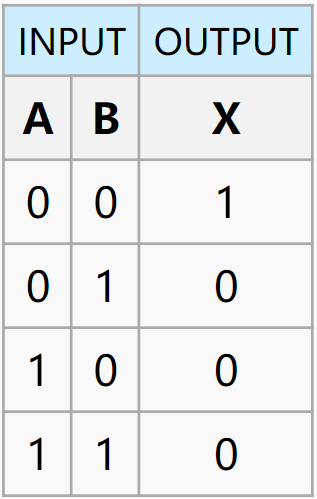 |
| XOR |  |
$out = A\oplus B$ | 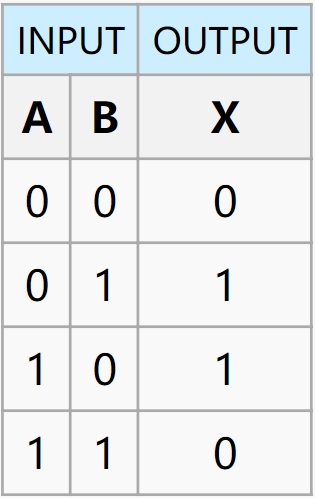 |
| XNOR |  |
$out = \overline{A\oplus B}$ | 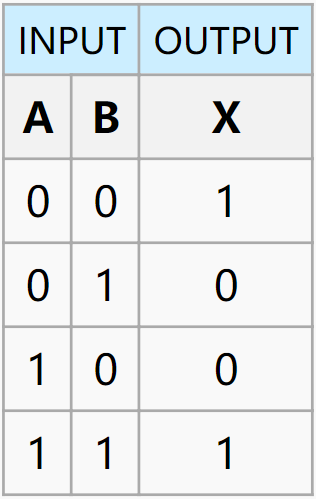 |
3.3 例题
第一题:
How many ordered-4-tuples (A, B, C, D) make the following circuit TRUE?
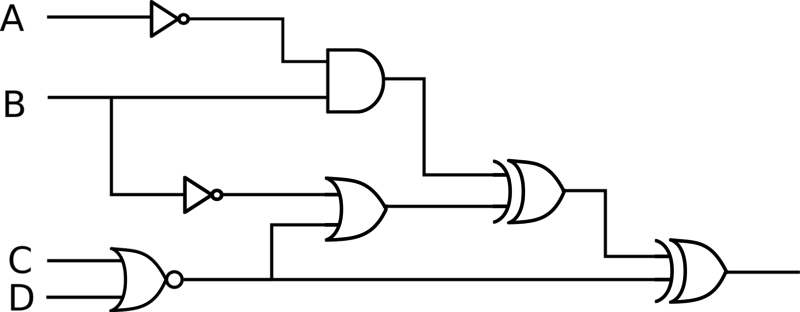
解答:
第一步: 将图片翻译为 Boolean Expression
第二步: 将 Boolean Expression 化简(用上一场的知识)
第三步: 列表枚举(和 Boolean Expression那个专题一样的操作)
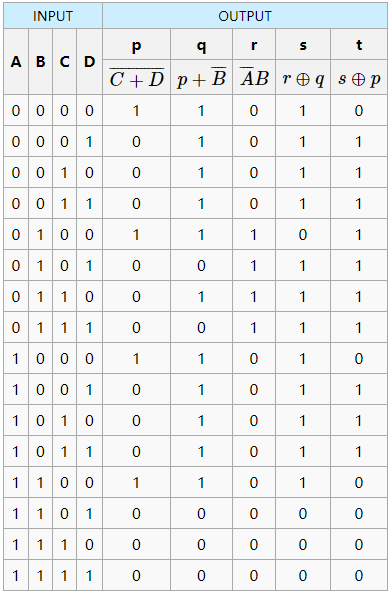
3.4 练习
3.4.1 Intermediate
题目
答案
3.4.2 Senior
题目
答案
4. 讲义下载
这个版本的 ACSL 讲义由 Rita Tan, 马润铎 的历史版本改编而来
