报告错误
如果你发现该网页中存在错误/显示异常,可以从以下两种方式向我们报告错误,我们会尽快修复:
- 使用 CS Club 网站错误 为主题,附上错误截图或描述及网址后发送邮件到 286988023@qq.com
- 在我们的网站代码仓库中创建一个 issue 并在 issue 中描述问题 点击链接前往Github仓库
1. 布尔代数 Boolean Algebra
在上一轮中,我们在 Bit String Flickering 中已经接触过二进制字符串的操作并了解了 AND,OR,XOR,NOT 这些基本的逻辑运算符。这次我们不会对包含很多位的二进制字符串做操作,而是对单个布尔值做逻辑运算操作。
1.1 布尔代数运算符
| 运算符 | 含义 |
|---|---|
| $A + B$ | $A$ OR $B$ |
| $A * B$ | $A$ AND $B$ |
| $A \oplus B$ | $A$ XOR $B$ |
| $\bar{A}$ | NOT $A$ |
在一些情境下,我们会省略两个布尔变量之间的 $*$ 号,例如直接将 $A * B$ 写为 $AB$
1.2 布尔代数化简求值
那么在只有一位的时候我们如何对表达式进行化简与求值呢?这就要求我们要把布尔代数表达式划分成一个个小的表达式分别进行求值和推断了。
1.2.1 使用 AND, OR 的特性求值
如果我们有两个未知的布尔值变量 $A$ ,虽然我们不能确定他的值,但是我们依然可以对以下这些式子进行化简求值……
| 布尔代数表达式 | 求值结果 | 解释 |
|---|---|---|
| $A + 1$ | 1 | 虽然不知道 $A$ 是 0 还是 1,任何布尔值与1进行 OR 操作的结果都是 1,所以这个式子的值是常量 1 |
| $A + \bar{A}$ | 1 | 虽然我们不知道 $A$ 的值,但是 $A$ 和 $\bar{A}$ 中至少有一个是 1,另一个是 0,所以两个值 OR 的结果是 1 |
| $A * 0$ | 0 | 无论 $A$ 是什么,与 0 做 AND 操作的结果只能是 0 |
| $A * \bar{A}$ | 0 | 无论 $A$ 是什么,$A$ 与 $\bar{A}$ 中一定有一个是 0,0 与任何值进行 AND 计算结果都是 0 |
1.2.2 布尔运算优先级
和普通的四则运算一样,布尔运算也是有优先级的,布尔运算的优先级遵从下面这个顺序
NOT > AND > XOR > OR
用布尔运算的符号表示,则有
\[\bar{} > * > \oplus > +\]1.2.3 布尔运算法则
对于普通的四则运算,我们有交换律,结合律和分配律等运算法则。对于布尔运算,我们也有类似的运算法则
分配律
\[A * (B + C) \leftrightarrow AB + AC\]结合律
\[A*B*C \leftrightarrow A * (B*C)\]交换律
\[A + B \leftrightarrow B + A\\ A * B \leftrightarrow B * A\]除此之外,还有一些特殊的运算法则是四则运算中没有的,例如
DeMorgan’s Law
\[\overline{A + B} \leftrightarrow \overline{A} * \overline{B}\] \[\overline{A * B} \leftrightarrow \overline{A} + \overline{B}\]异或化简法则(异或的定义)
\[A \oplus B \leftrightarrow A\overline{B} + \overline{A}B\] \[\overline{A \oplus B} \leftrightarrow AB + \overline{A}*\overline{B}\]1.3 例子
在实际运算中,1.2.3 的运算法则要和 1.2.1 中的求值结合起来使用,只有这样才能将布尔代数表达式化简到最简形式。下面我们用两个例子来说明如何做 ACSL 中布尔代数的相关题目
例1 Simplify the following expression $A(A + BC) + B(B + AC)$
Solution
\[\begin{aligned} &= A + ABC + B + BAC \\ &= A + ABC + B\\ &= A + B(AC + 1)\\ &= A + B \end{aligned}\]这里我们用到了一个技巧 - 一个单独的变量 $A$ 可以看作 $A * 1$ 的结果,类似的,在一些情况下你也可以把 $A$ 看作 $A + 0$ 的结果。
例2 How many pairs / List all the pairs of ABC that make the following expression FALSE
\[\overline{AB} + A\overline{B + C}\]遇到这种题的时候我们先将给定的表达式进行化简
\[\begin{aligned} &= \bar{A} + \bar{B} + A * (\bar{B} * \bar{C}) \\ &= \bar{A} + \bar{B} * (1 + A\bar{C})\\ &= \bar{A} + \bar{B} \end{aligned}\]在进行完化简后我们再将所有的 ABC 取值列一张表格进行求值
| $A$ | $B$ | $C$ | $\bar{A} + \bar{B}$ |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 |
列出这张表后,我们可以看到当 $A, B, C$ 等于 $(1, 1, 1)$ 和 $(1, 1, 0)$ 时,$\bar{A} + \bar{B}$ 的值时 FALSE。
1.4 练习
1.4.1 Intermediate
题目
答案
1.4.2 Senior
题目
答案
2 数据结构 Data Structure
对一个程序来说,算法和数据结构必不可少。ACSL中考察的数据结构主要有以下几种:
- Queue 队列
- Stack 堆栈
- Binary Search Tree 二分查找树
- Priority Queue 优先队列
2.1 队列与堆栈 Queue & Stack
队列指遵循 FIFO (First in First Out) 的规则。先进入队列的对象会先被取出来。堆栈遵循 FILO (First in Last Out)的规则,先进入堆栈的对象会后被取出来。 队列和堆栈有的时候也被称为 FIFO Stack 和 FILO Stack。
常见的 Queue / Stack 操作有以下几种:
- $PUSH(N)$ 将 $N$ 放入 数据结构中
- $POP()$ 从数据结构中取出对象
- $REVERSE()$ 将现在数据结构中的对象顺序反转
- $SWITCH()$ 将当前数据结构切换为 Stack / Queue
2.1.1 PUSH(N) & POP(X) 方法
例1:Stack
\[PUSH(A), PUSH(B), POP(X), PUSH(C)\]What will be the next element pop out of stack?
解:
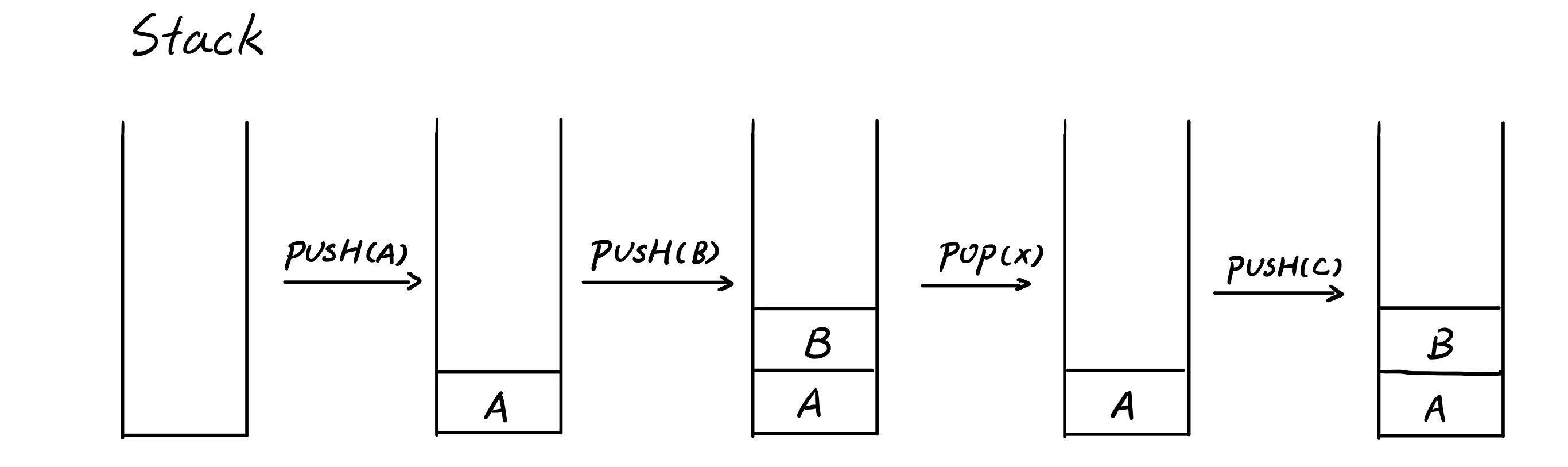
下一个被 POP 出 Stack 的是 $B$。
2.1.2 REVERSE() 方法
反转当前数据结构内所有的对象顺序
例2:Queue \(PUSH(A), PUSH(N), REVERSE(), POP(X), PUSH(B)\) What will be the next element pop out of queue?
解:
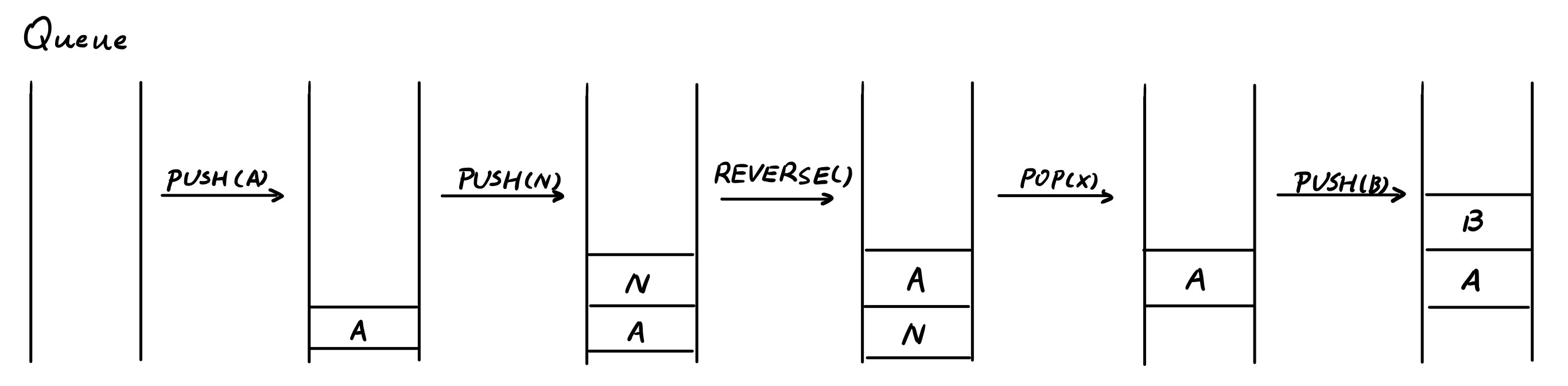
下一个被 POP 出 Queue 的是 $A$
2.1.3 SWITCH() 方法
如果现在数据结构是 Stack,执行完 SWITCH() 后数据结构变为 Queue,内部对象顺序不变,反之亦然。
2.2 二分查找树 Binary Search Tree
二分查找树是一种数据结构,也是一种树(无环图)。
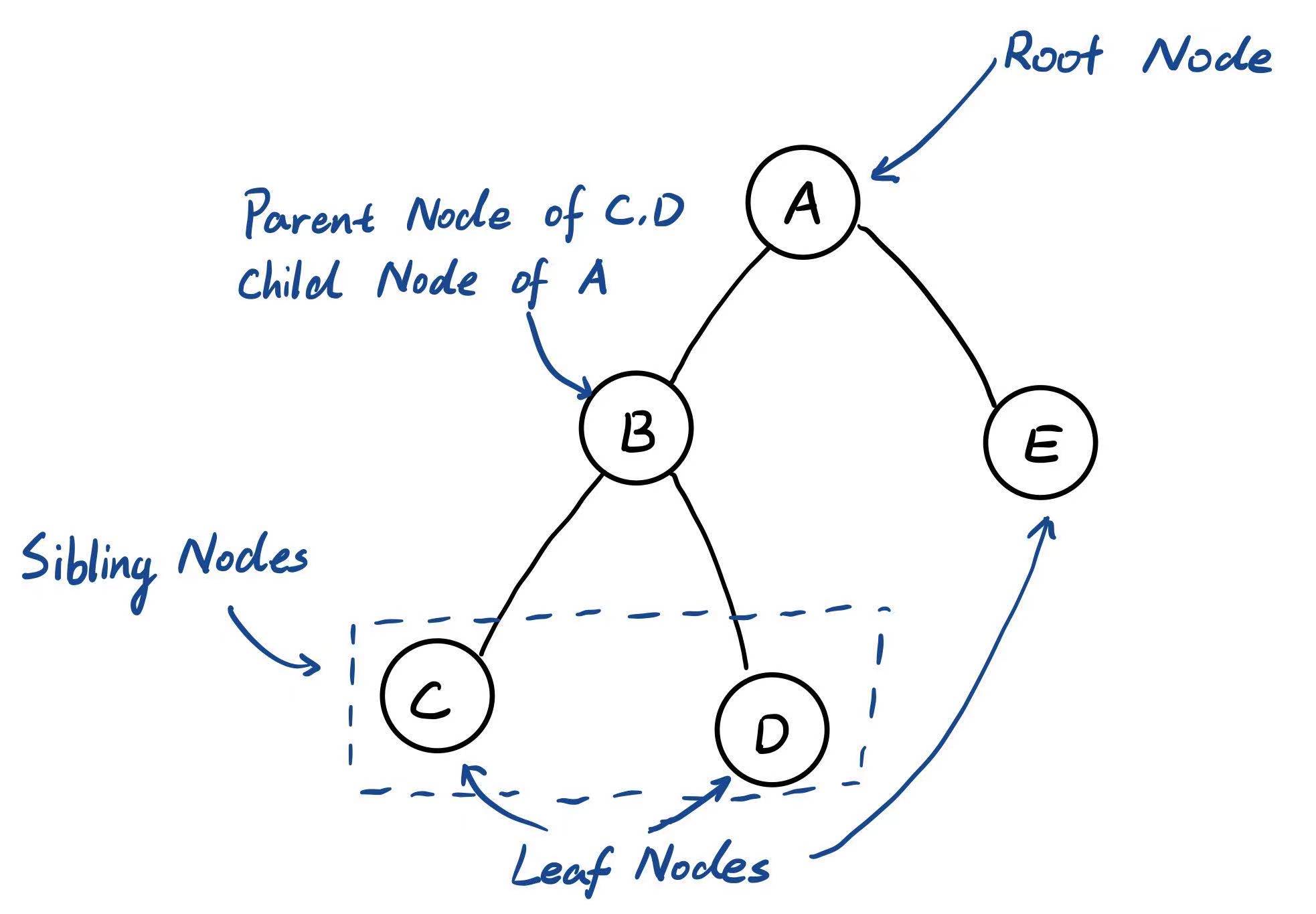
2.2.1 图论:树的术语
- 根节点 (Root Node) - 最顶端的节点
- 父节点 (Parent Node) 下面直接相连的节点叫做子节点 (Child Node)
- 有同一个父节点的节点称为兄弟节点(Sibling Node)
- 每个分支最底部的节点被称为叶子节点 (Leaf Node),叶节点没有子节点
2.2.2 二分查找树的性质
二分查找树的每个节点有三个属性 - 节点的值 (key) ,指向左侧子节点的指针 (left child pointer),指向右侧子节点的指针 (right child pointer)
在一个排好序的二分查找树中,每个节点的 key 比左子节点的 key 大(如果存在左子节点),比右子节点的 key 小(如果存在右子节点)
重复的 key 小于原有的 key。也就是说如果 key "A" 在BST中出现了两次,那么第二次的A一定在第一次出现的A的节点的左侧
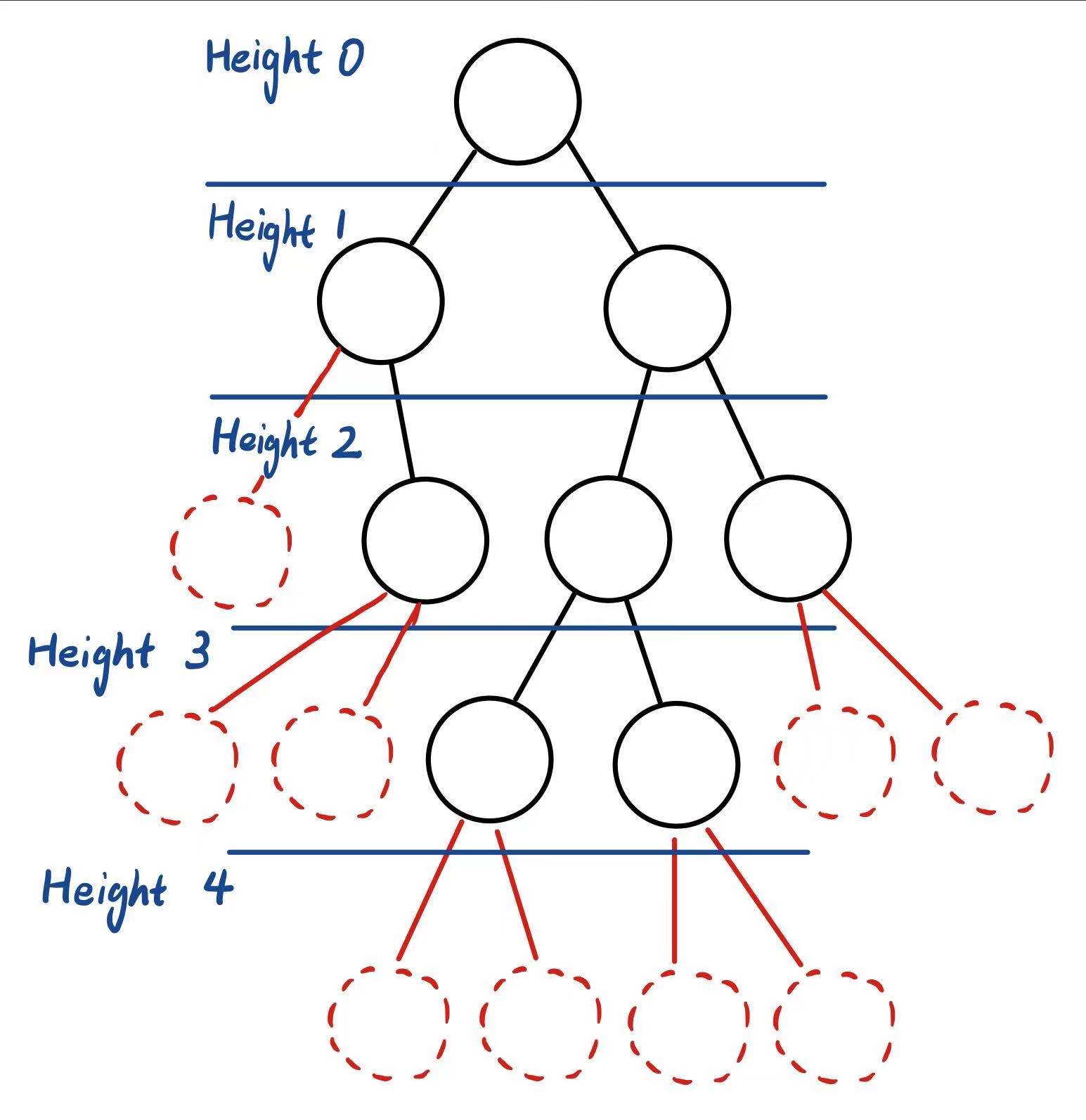
2.2.3 二分查找树的属性
| 属性 | 解释 |
|---|---|
| Depth | 距离根节点最远的叶子节点的高度(根节点高度为0) |
| Internal Path Length | 所有节点的深度之和 |
| External Path Length | 所有可加入二分查找树的位置的高度之和 |
例1:
2.3.4 二分查找树的遍历输出 (Traverse)
有三种方法遍历一个二分查找树 - Inorder, Preorder, Postorder
- Inorder - 先描述树的左子树,然后描述根节点,最后描述右边的子树
- Preorder - 先描述树的根节点,然后描述树的左,右节点
- Postorder - 先描述左子树,然后描述右子树,最后描述根节点
拿这颗树作为例子:
- Inorder 描述:C,B,D,A,E
- Preorder 描述:A,B,C,D,E
- Postorder 描述:C,D,B,E,A
对一个平衡树可以做 Insert, Delete 和 Search 的操作,也可以通过这些操作将它排列为平衡树。
2.4 优先队列 Priority Queue
2.4.1 优先队列特性
优先队列和二分查找树有一定程度上的相似,但是只能从 PQ 中 search 或 delete 最小的值,类似 BST 中的 Root。优先队列通常使用二分最小堆 (Binary Min Heap) 实现,二分最小堆使用一个类似二分搜索树的结构,同时使这个树保持:
- 每个 node 的 children 的值一定比它自己的值小 (如果有 children),但是 Children 之间的大小关系没有限制
- 整个树没有 holes,也就是说除了最底层以外的其他地方都要排满,最底层从左到右排满,中间没有空隙
Priority Queue 可以进行 push, pop 的操作。
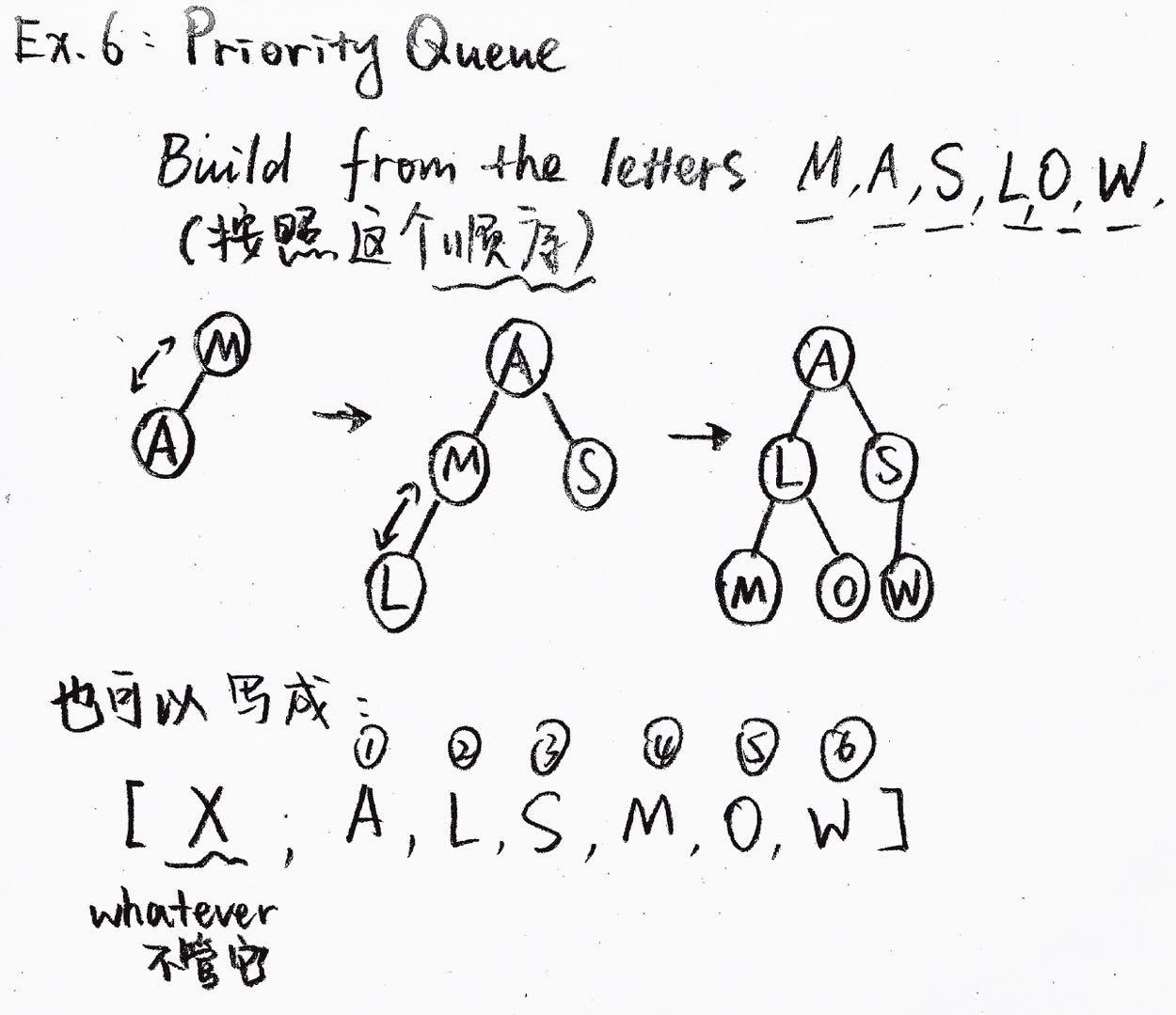
2.4.2 优先队列表达
和二分查找树类似,优先队列也可以写成一个线性的列表形式,并且通过列表的索引来确定节点在二分最小堆中的位置。
2.5 练习
2.5.1 Intermediate
题目
答案
2.5.2 Senior
问题
答案
3 正则表达式与有限状态机 RegEx and FSA
3.1 介绍
FSA (Finite State Automaton,有限状态机) 是一种表示模型状态的计算模型,通常以有向图的形式表达。有向图中的每个节点是模型的一种可能状态,两个状态之间的有向边表示模型从一个状态变化为另一个状态的变化。
正则表达式是一种用来描述文字模式匹配规则的语言。这种语言让我们可以使用线性的文字描述一个用于匹配字符串的有限状态机。RegEx - Wikipedia
3.2 正则表达式
3.2.1 正则表达式语法
正则表达式是一个字符串,其中有一些特定的符号({, }, |, ^, [, ], +, *, . 等)具有特殊含义。下面我会举例子说明每个符号的含义
| 符号 | 含义 | RegEx 例子 | 能够被RegEx匹配到的字符串例子 |
|---|---|---|---|
| |
或 | mark|Mark |
“mark”, “Mark” |
* |
出现 0 或多次 | gr*eat |
“geat”, “great”, “grreat”, …., “grr….rreat”, etc. |
+ |
出现 1 或多次 | ab+c |
“abc”, “abbc”, “abb…bc”, etc. |
. |
代表任意字符 | m.rk |
“mark”, “mbrk”, “m[rk”, etc. |
[] |
代表字符范围 | m[a-d]rk |
“mark”, “mbrk”, “mcrk”, “mdrk” |
^ |
否定(取反) | m[a-d^]rk |
“merk”, “mfrk”, etc. |
() |
一个子正则表达式 | m(a*|b)rk |
“maaaark”, “mbrk”, “mrk”, “mark”, etc. |
λ |
空字符串 |
通过组合这些符号,我们可以制定出非常复杂的匹配规则。
* 实际上正则表达式还有很多强大的符号,例如
\d表示任意数字等,不过这些与具体的正则表达式实现有关,并且也不在ACSL考察范围内,具体使用可以查询自己用的语言的 regex 文档。
3.2.2 正则表达式化简
在上面描述符号的时候,可能你已经发现有一些情况下我们可以化简正则表达式,通过合并/消除冗余的部分,我们可以提高正则表达式的匹配性能和可读性。
下面会介绍一些正则表达式的化简规则与恒等式
| 规则 | 解释 |
|---|---|
(a*)* $\leftrightarrow$ a*
|
0 到多次出现(0到多次出现 a) $\rightarrow$ 0 到 多次出现 a |
aa* $\leftrightarrow$ a*a $\leftrightarrow$ a+
|
a(), a(a), a(aa), a(aaa), … $\leftrightarrow$ ()a, (a)a, (aa)a, (aaa)a, … |
a+|λ $\leftrightarrow$ a*
|
空字符串或者a出现1或多次 $\leftrightarrow$ a 出现0或多次 |
a(b|c) $\leftrightarrow$ ab|ac
|
a一定出现,接着是 b 或 c $\leftrightarrow$ ab 或 ac |
(a|b)*$\leftrightarrow$(a*|b*)* $\leftrightarrow$ (a*b*)*
|
a, b 交替出现零或多次,不限顺序 |
这里安利一个非常好用的网站,可以检测正则表达式的匹配结果 RegEx 101
3.3 有限状态机 Finite State Automaton
3.3.1 有限状态机的性质
有限状态机有以下几个性质
- 有限数量的状态
- 有状态转移规则
- 只有一个初始状态
- 有一个或多个结束状态
3.3.2 有限状态机的表达
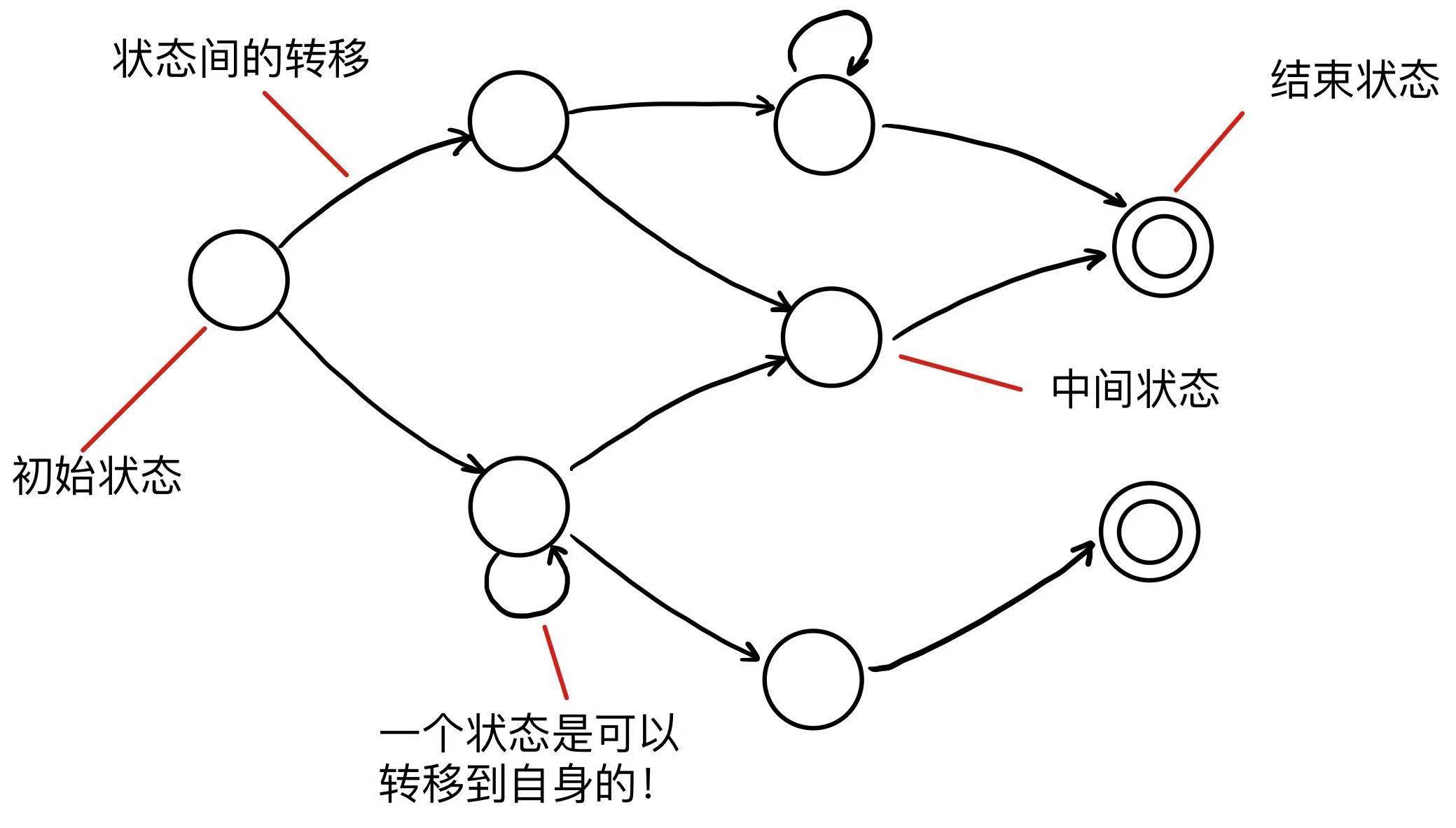
我们使用一个有向图来表示一个 FSA,空心圆(节点)代表一个状态,节点之间的连线代表状态之间的转移,最后的同心圆表示结束状态。
3.4 RegEx 与 FSA 互相转化
RegEx的初始状态是空字符串 - 没有字符串被匹配到,每个 Regex 字符被翻译为状态之间的转移过程,如果匹配过程最后到达了结束状态,说明这个字符串可以被 RegEx 所描述的模式匹配到。
每次遇到 | 时,FSA会在当前状态下产生两个可能的状态转移(分叉)。
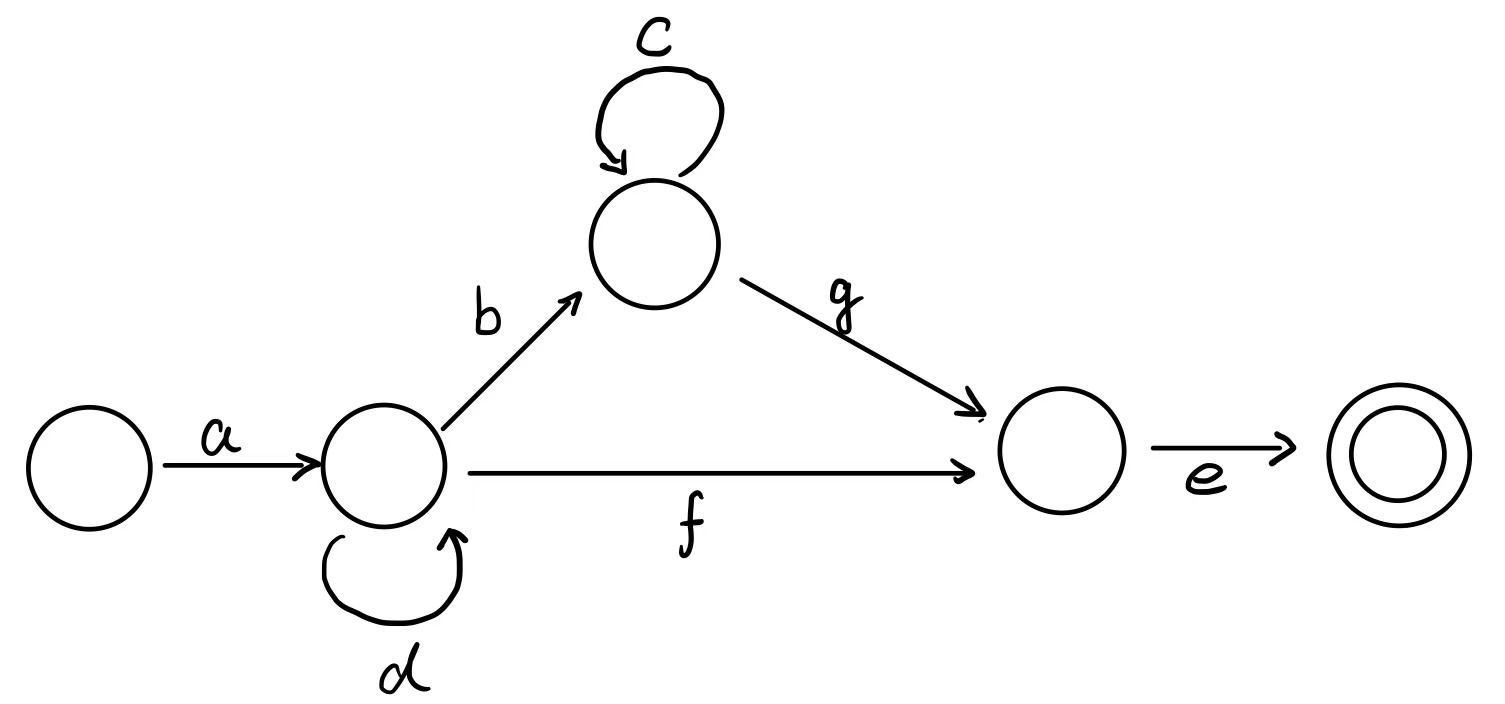
例1
假设我们想将这样一个 RegEx 转化为 FSA
ad*(bc*g|f)e结果大概是这样的:
3.5 练习
3.5.1 RegEx
题目
答案
3.5.2 FSA
问题
答案