神经网络如何工作

Neural Network

---

Mark Chen | 31 Jul 2020

报告错误

如果你发现该网页中存在错误/显示异常，可以从以下两种方式向我们报告错误，我们会尽快修复：

1. 使用 CS Club 网站错误 为主题，附上错误截图或描述及网址后发送邮件到 286988023@qq.com
2. 在我们的网站代码仓库中创建一个 issue 并在 issue 中描述问题 点击链接前往Github仓库

神经网络作为一种新兴的计算机技术被许多人称为一种全新的“编程范式”，与往常的算法编写不同，神经网络是一种“数据驱动”的编程方法。在往常的算法编写中，人们需要手动编写算法的逻辑，而在神经网络中，人们只需要为网络提供海量数据和参考答案，网络就会自动生成算法。那么神经网络到底是怎么工作的呢？

By Mark Chen, 29299731

这篇文章会对机器学习中的神经网络为什么可以被训练&输出正确预测做出不严谨但直观的解释。

0. 模型是一个函数

我们可以将一个深度学习中的模型看做一个映射关系： \(\text{Perception} \rightarrow \text{Output}\) 对于一个深度学习模型是“感知”（模型可以获得的所有信息的总和）与一个“数字”或者 “决策”之间的映射关系。所以我们可以将模型看作一个函数$F(x)$.

那么模型就可以被表示为：$F(\text{Perception}) =\text{Output}$

Example: Alpha Go 可以被表示为 $F(\text{棋盘状态}) = 当前落子最优位置$ 这样一个函数

现在我们假设有这样的一个函数：对于任何定义域内的输入都一定会给出此时的最优输出。这样的一个理想函数我们记作$G(x)$(Ground Truth)。 当我们“训练”模型$F(x)$的时候，我们的目标就是让模型尽可能拟合$G(x)$。也就是说，我们想要通过训练使得我们的模型$F(x)$ 的输出与事实（最优函数）$G(x)$的差距最小化。

1. 什么是神经网络

要知道为什么”神经网络“可以被用来拟合函数呢？首先我们先了解一下什么是“神经网络”。

神经网络由许多神经元相互连接而组成，每个神经元都有自己的参数$\theta$ 。我们可以将神经元描绘为一个函数 $f(\theta_i, x) = y$。那么对于下面一个模型（$F(\Theta, x), \quad \Theta=\lbrace \theta_1, \theta_2, \dots, \theta_n\rbrace$），我们可以写出它的数学表达式：

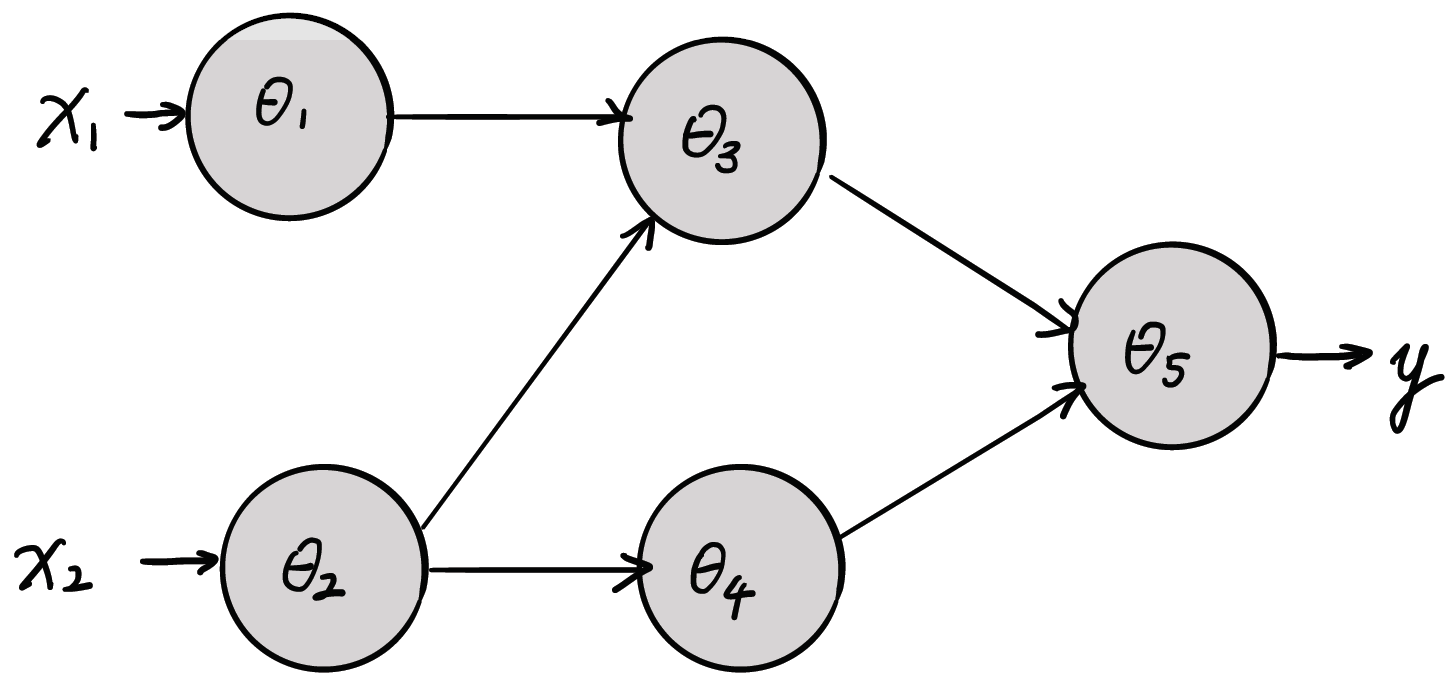
\(F(\Theta, x) = f(\theta_5, (f(\theta_3, f(\theta_2, x_2) + f(\theta_1, x_1)), f(\theta_4, f(\theta_2, x_2))))\) 从上面的式子我们可以看到参数$\theta$的取值和模型本身的结构（上图中函数互相嵌套的关系）共同决定了模型的最终输出。

2. 神经网络可以拟合函数

神经网络的本质建立在这样一个事实上：简单非线性函数的重复的迭代与叠加可以在拥有适当参数的情况下有限精度的拟合任何连续函数。下面的例子会给出一个直观但不严谨的，对神经网络拟合二元函数的证明：

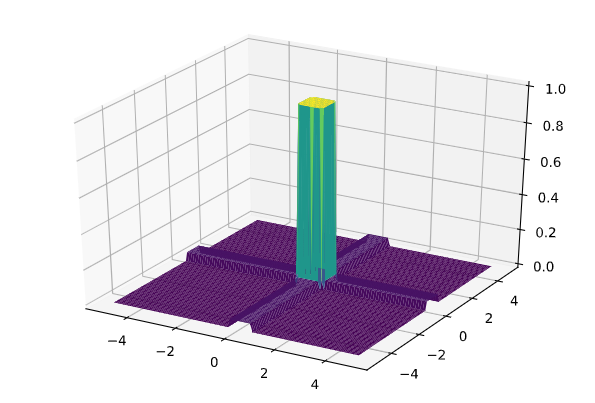
首先，我们可以用5个使用sigmoid函数的神经元来构建一个“高台”函数。(代码是具体的实现)

import matplotlib.pyplot as plt
import numpy as np
import pylab
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

def sigmoid(x):
    s = 1 / (1 + np.exp(-x))
    return s

def tower(x, y, x_min, x_max, y_min, y_max):
    x1 = sigmoid(1000 * (x - x_min))
    x2 = sigmoid(1000 * (x - x_max))

    y1 = sigmoid(1000 * (y - y_min))
    y2 = sigmoid(1000 * (y - y_max))

    z = x1-x2+y1-y2
    z = sigmoid(30*(z-1.1))
    return z


X = np.arange(-5, 5, 0.1)
Y = np.arange(-5, 5, 0.1)
X, Y = np.meshgrid(X, Y)
Z = tower(X, Y, -0.3, 0.7, -0.2, 0.8)
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)
plt.show()

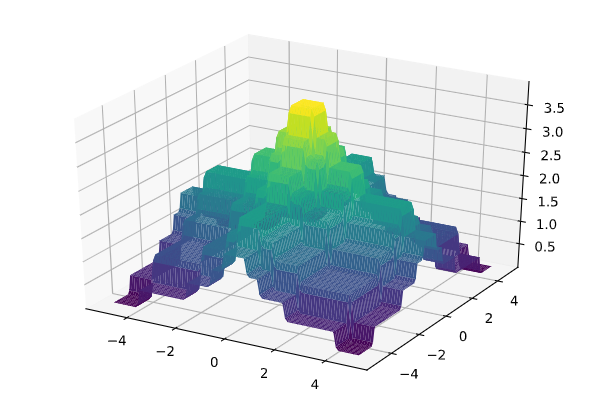
如果我们把这样的一个高台记作$Tower(x_1, x_2，\Theta)$，那么通过组合足够多这些高台，我们可以得到任何一个连续二元函数的任意小精度拟合（缩小每个高台的面积），例如下图（左：原函数，右：四个$Tower(x_1, x_2,\Theta)$的组合

def tower(x, y, x_min, x_max, y_min, y_max):
    x1 = sigmoid(1000 * (x - x_min))
    x2 = sigmoid(1000 * (x - x_max))

    y1 = sigmoid(1000 * (y - y_min))
    y2 = sigmoid(1000 * (y - y_max))

    z = x1-x2+y1-y2
    z = sigmoid(4*(z-1.1))
    return z

Z = tower(X, Y, -0.5, 0.5, -0.5, 0.5) + tower(X, Y, -1, 1, -1, 1) + tower(X, Y, -2, 2, -2, 2) + tower(X, Y, -4, 4, -4, 4)
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)
plt.show()

3. 如何让电脑自动调参？

在上面的例子中，所有的参数都是人工设定的，因为只有20个不到的参数，人工设定是一种可行的做法。可是目前绝大多数的模型都有超过一万个参数，参数最多的自然语言模型GPT-3甚至有1730亿个参数（存储整个模型需要800T空间）！在这么多参数的情况下，人工调节每一个参数变成了一项不可能的任务，所以我们需要让电脑来自动调整参数来让模型$F(x)$拟合到目标$G(x)$上。

要让电脑自动完成这项工作，我们需要先回想一下当我们调整参数时我们所作的工作：

1. 评估现在的模型$F(x)$与$G(x)$相差大不大（现在的模型是不是一个好模型）

2. 预测调节参数$\theta$（调大/调小）以后模型会变好还是变坏

3. 如果参数$\theta$调小可以让模型$F(x)$更加接近$G(x)$，那么就调小$\theta$， 反之亦然

损失函数

为了让机器拥有完成任务1的能力，人们设计出了“损失函数”用来量化表示模型$F(x)$与事实$G(x)$之间的差距，用$L(\hat{y}, y)$表示，$\hat{y}$表示模型的输出（对Ground Truth $y$的预测值），一般来说，一个良好的损失函数应该有这些性质：

1. 损失函数大小与模型质量单调递增 - 模型越差，损失函数越大
2. 损失函数应该是一个连续，尽量平滑的函数

一种常见的损失函数是$L(\hat{y}, y) = (y - \hat{y})^2$

参数调节方向的计算

为了让机器完成任务2 和 3，我们需要将”预测调节参数$\theta$（调大/调小）以后模型会变好还是变坏“这样一个主观的过程用数学方法表达出来。因为我们已经引入了损失函数，所以实际上这个过程可以被表述为“预测如何调节参数$\theta$（调大/调小）可以减小损失函数的值”

在此之前，我们先看一看我们如何最小化一个一元函数$h(x)$. 对于一个一元函数，我们可以计算出当前位置的一阶导数$dh/dx$。如果一阶导数是正数，说明增大$x$可以增大$h(x)$，反之亦然。所以要最小化$h(x)$，我们只需要不停的执行下面这一个操作： \(x\stackrel{\text{update}}{\longrightarrow}x - \eta \cdot \frac{dh(x)}{dx},\quad\quad \text{where $\eta$ is a positive number}\) 这里的$\eta$是一个参数“学习速率”，学习速率越高，每次更新$x$的时候$x$的值就会改变越多 。

有了上面的铺垫，解决“预测如何调节参数$\theta$（调大/调小）可以减小损失函数的值”的方法就很明显了：计算$\partial L(\hat{y}, y)/\partial \theta$ 并且将$\theta$按照一下方式更新： \(\theta\stackrel{\text{update}}{\longrightarrow}\theta - \eta \cdot \frac{\partial L(\hat{y}, y)}{\partial\theta},\quad\quad \text{where $\eta$ is a positive number}\)

有些人可能会疑惑，在$L(\hat{y}, y)$中明明都没有自变量$\theta$ 啊，怎么计算$\frac{\partial L(\hat{y}, y)}{\partial \theta}$ 呢？

实际上注意到损失函数的第一个输入时$\hat{y}$，也就是模型的输出，而模型可以表示为$F(\theta, x)$，所以我们可以通过链式法则计算$\frac{\partial L(\hat{y}, y)}{\partial\theta}$ \(\frac{\partial L(\hat{y}, y)}{\partial \theta} = \frac{\partial L(\hat{y}, y)}{\partial \hat{y}}\cdot \frac{\partial \hat{y}}{\partial \theta}\)

这也是神经网络的基石 - 反向传播算法 (Back Propagation) 的数学原理

当机器拥有了自动更新权重的能力的时候，我们就可以开始对神经网络进行训练了！训练的过程其实就是将样本从训练数据集中输入到模型中，再通过算法自动调节模型函数来最小化损失函数。

评论区